Create space-filling curves

Usage

sfc_2x2(seed, code = integer(0), rot = 0L)

sfc_3x3_peano(seed, code = integer(0), rot = 0L, level = NULL, flip = FALSE)

sfc_3x3_meander(seed, code = integer(0), rot = 0L, flip = FALSE)

Arguments

seed: The seed sequence. In most cases, the seed sequence is a single base pattern, which can be specified as a single letter, then rot controls the initial rotation of the base pattern. It also supports a sequence with more than one base patterns as the seed sequence. In this case, it can be specified as a string of more than one base letters, then rot can be set to a single rotation scalar which controls the rotation of the first letter, or a vector with the same length as the number of base letters.
code: A vector of the expansion code. The left side corresponds to the top levels of the curve and the right side corresponds to the bottom level of the curve. The value can be set as a vector e.g. c(1, 2, 1), or as a string e.g. "121", or as a number e.g. 121.
rot: Rotation of the seed sequence, measured in the polar coordinate system, in degrees.
level: Specifically for sfc_3x3_peano(), since there is only one expansion code 1, it can also be generated by rep(1, level).
flip: Whether to use the "flipped" rules? For the Peano curve and the Meander curve, there is also a "fliiped" version of curve expansion rules. On each level expansion in the Peano curve and the Meander curve, a point expands to nine points in 3x3 grids. Thus the value of flip can be set as a logical vector of length of nine that controls whether to use the flipped expansion for the corresponding unit. Besides such "1-to-9" mode, flip can also be set as a function which acccepts the number of current points in the curve and return a logical vector with the same length, i.e. the "all-to-all*9" mode.

Value

sfc_hilbert() returns an sfc_2x2 object.
sfc_peano() returns an sfc_3x3_peano object.
sfc_meander() returns an sfc_3x3_meander object.

These three classes are child classes of sfc_nxn.

Details

sfc_2x2() generates the Hilbert curve from the seed sequence.
sfc_3x3_peano() generates the Peano curve from the seed sequence.
sfc_3x3_meander() generates the Meander curve from the seed sequence.

Examples

sfc_2x2("I", "111") |> plot()

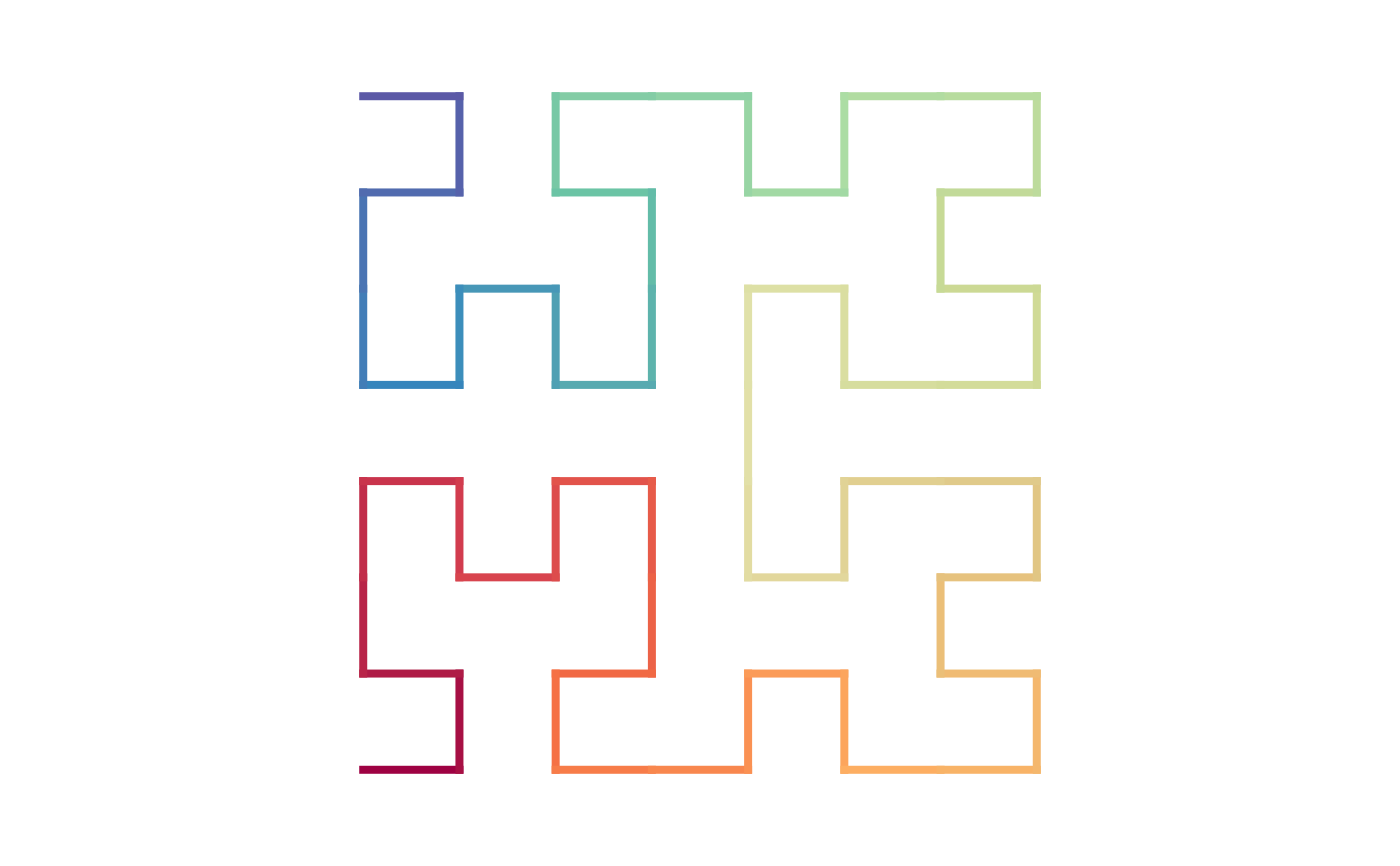sfc_2x2("I", "111", rot = 90) |> plot()

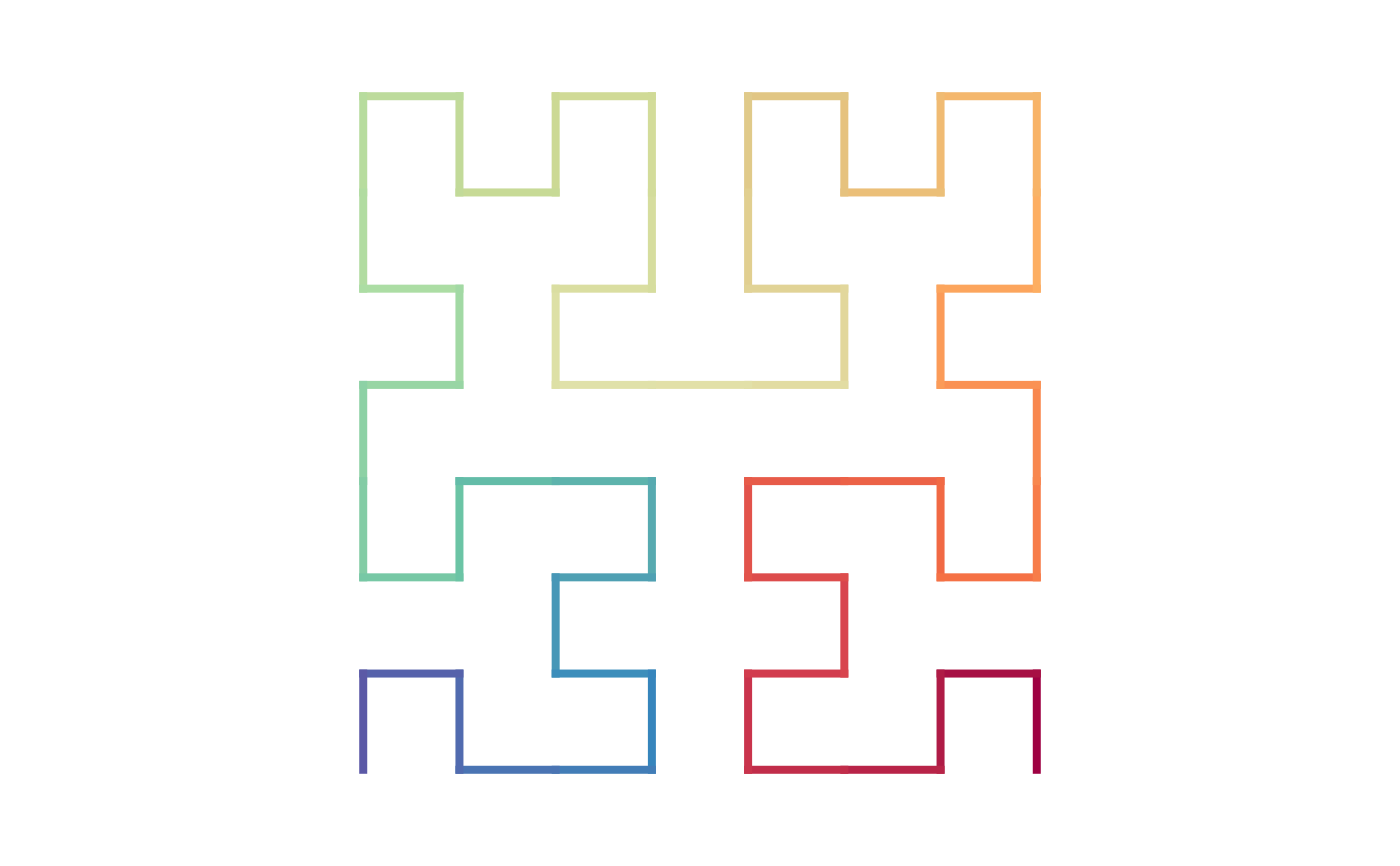sfc_2x2("IR", "111", rot = 90) |> plot()

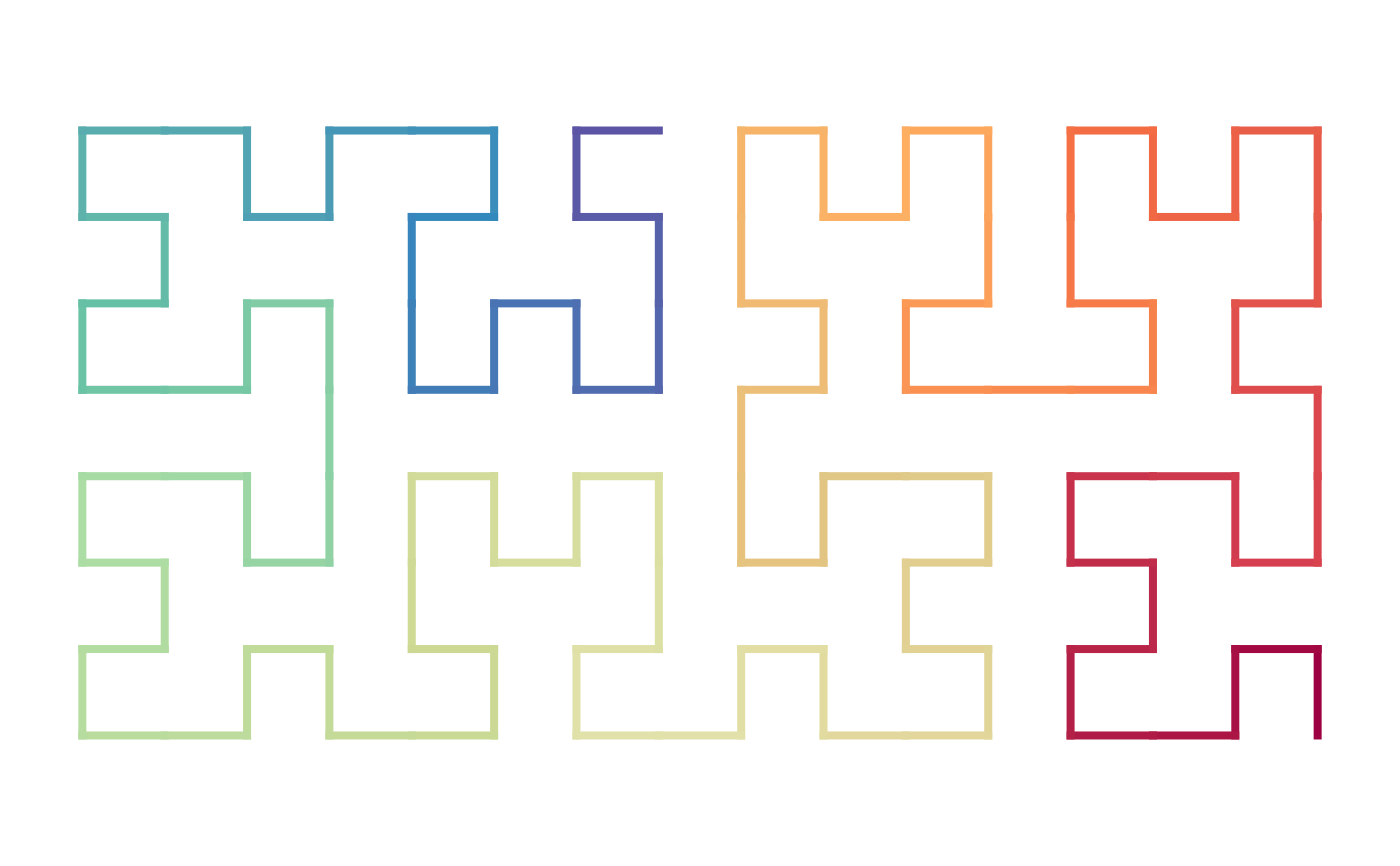sfc_3x3_peano("I", "111") |> plot()

sfc_3x3_peano("I", "111", 
    flip = c(FALSE, FALSE, FALSE, TRUE, FALSE, FALSE, TRUE, FALSE, FALSE)) |> plot()

sfc_3x3_peano("IJ", "111") |> plot()


sfc_3x3_peano("I", level = 4, flip = function(p) {
    p@rot %in% c(90, 270)
}) |> plot(lwd = 1)


level = 4
sfc_3x3_peano("I", level = level, flip = function(p) {
     if(length(p) == 9^(level-1)) {
         l = rep(FALSE, length(p))
         ind = 1:9^2 + 9^2*rep(c(0, 2, 4, 6, 8), each = 9^2)
         l[ind] = p@rot[ind] %in% c(90, 270)

         ind = 1:9^2 + 9^2*rep(c(1, 3, 5, 7), each = 9^2)
         l[ind] = p@rot[ind] %in% c(0, 180)

         l
    } else {
         rep(FALSE, length(p))
    }
}) |> plot(lwd = 1)


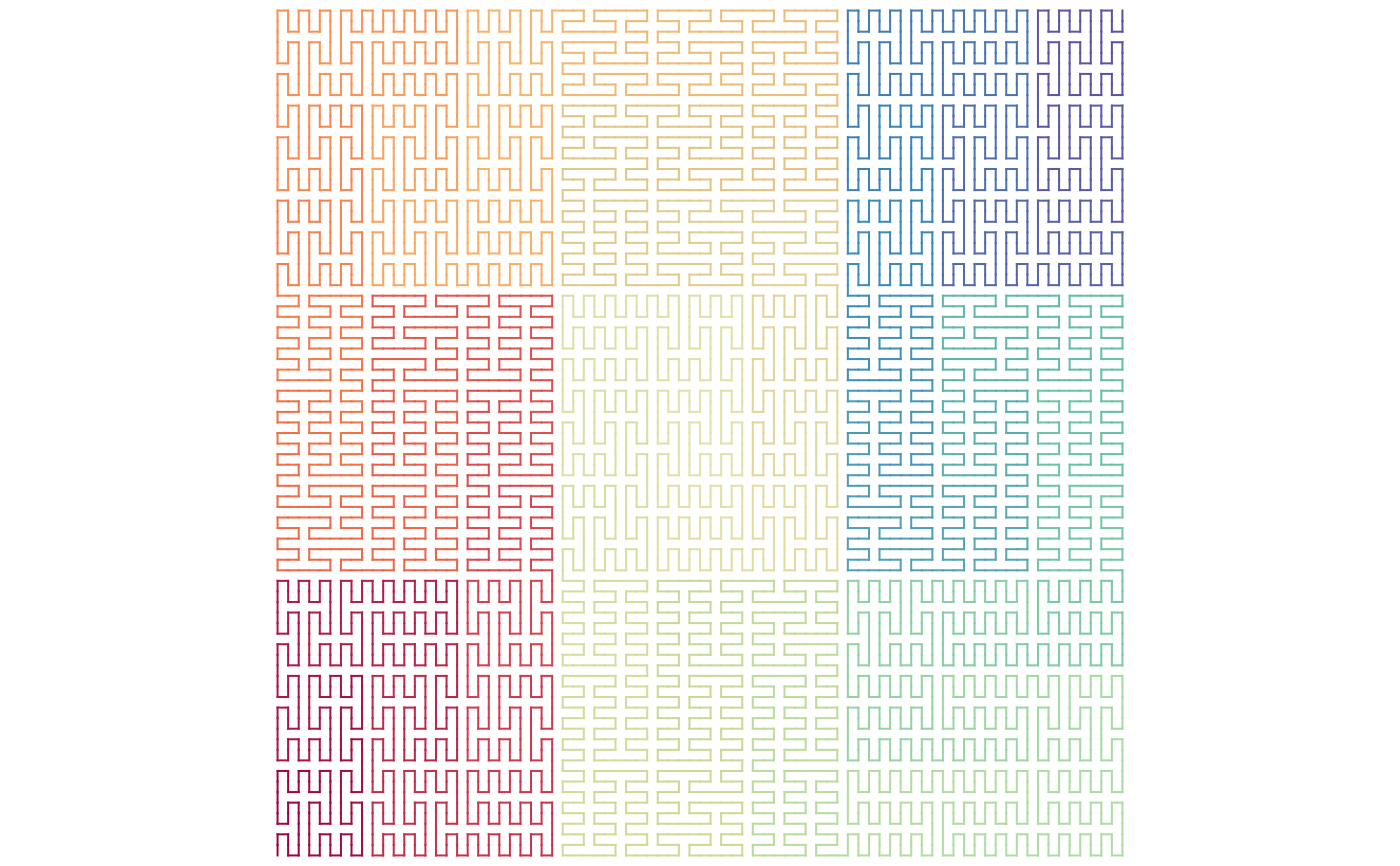sfc_3x3_meander("I", "111") |> plot()

sfc_3x3_meander("I", "111", 
    flip = c(TRUE, FALSE, TRUE, FALSE, FALSE, TRUE, FALSE, FALSE, TRUE)) |> plot()

sfc_3x3_meander("IR", "111") |> plot()