Chapter 17 Make fun of the package
17.1 A clock
The first example is a clock. The key function here is circos.axis() (Figure
17.1). In the example, the whole circle only contains one sector in
which major tick at 0 is overlapping with major tick at 12.
Later we calculate the positions of the hour hand, the minute hand and the second hand
based on current time when this Chapter is generated. The hands are drawn by arraws() function
in the canvas coordinate. A real-time clock can be found at the Examples section in
the help page of circos.axis().
circos.par(gap.degree = 0, cell.padding = c(0, 0, 0, 0), start.degree = 90)
circos.initialize("a", xlim = c(0, 12))
circos.track(ylim = c(0, 1), bg.border = NA)
circos.axis(major.at = 0:12, labels = NULL, direction = "inside",
major.tick.length = mm_y(2))
circos.text(1:12, rep(1, 12) - mm_y(6), 1:12, facing = "downward")
current.time = as.POSIXlt(Sys.time())
sec = ceiling(current.time$sec)
min = current.time$min
hour = current.time$hour
sec.degree = 90 - sec/60 * 360
arrows(0, 0, cos(sec.degree/180*pi)*0.8, sin(sec.degree/180*pi)*0.8)
min.degree = 90 - min/60 * 360
arrows(0, 0, cos(min.degree/180*pi)*0.7, sin(min.degree/180*pi)*0.7, lwd = 2)
hour.degree = 90 - hour/12 * 360 - min/60 * 360/12
arrows(0, 0, cos(hour.degree/180*pi)*0.4, sin(hour.degree/180*pi)*0.4, lwd = 2)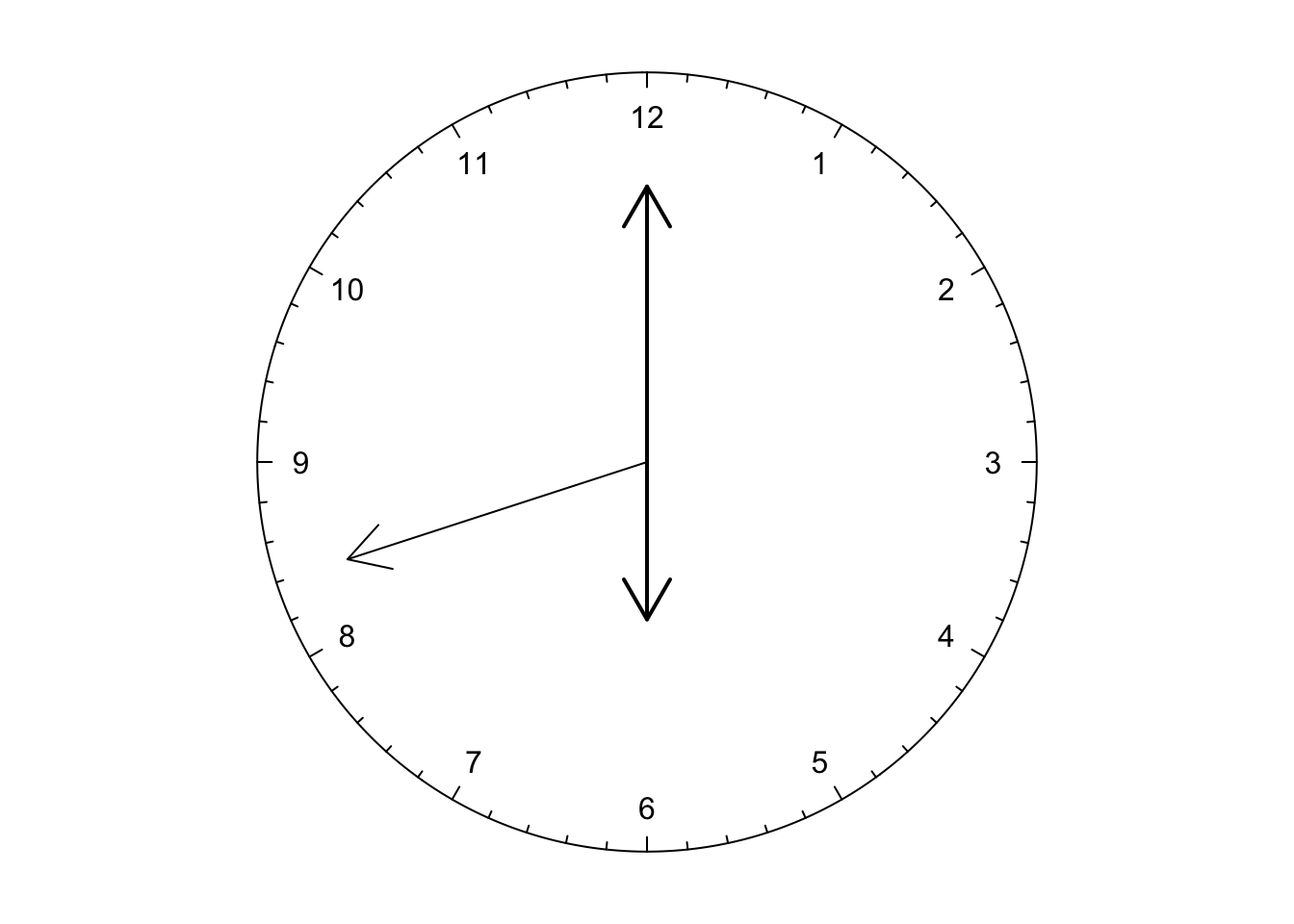
Figure 17.1: A clock.
circos.clear()17.2 A dartboard
The second example is a dartboard. In Figure 17.2, tracks are assigned with
different heights and each cell is initialized with different colors. The most
inside green ring and red circle are plotted by draw.sector().
We use circos.trackText() to add labels because we know the global order of the labels.
Now you can project the plot on your door and begin to play!
sectors = 1:20 # just indicate there are 20 sectors
circos.par(gap.degree = 0, cell.padding = c(0, 0, 0, 0),
start.degree = 360/20/2, track.margin = c(0, 0), clock.wise = FALSE)
circos.initialize(sectors, xlim = c(0, 1))
circos.track(ylim = c(0, 1), sectors = sectors, bg.col = "black", track.height = 0.15)
circos.trackText(x = rep(0.5, 20), y = rep(0.5, 20),
labels = c(13, 4, 18, 1, 20, 5, 12, 9, 14, 11, 8, 16, 7, 19, 3, 17, 2, 15, 10, 6),
cex = 0.8, sectors = sectors, col = "#EEEEEE", font = 2, facing = "downward")
circos.track(ylim = c(0, 1), sectors = sectors,
bg.col = rep(c("#E41A1C", "#4DAF4A"), 10), bg.border = "#EEEEEE", track.height = 0.05)
circos.track(ylim = c(0, 1), sectors = sectors,
bg.col = rep(c("black", "white"), 10), bg.border = "#EEEEEE", track.height = 0.275)
circos.track(ylim = c(0, 1), sectors = sectors,
bg.col = rep(c("#E41A1C", "#4DAF4A"), 10), bg.border = "#EEEEEE", track.height = 0.05)
circos.track(ylim = c(0, 1), sectors = sectors,
bg.col = rep(c("black", "white"), 10), bg.border = "#EEEEEE", track.height = 0.375)
draw.sector(center = c(0, 0), start.degree = 0, end.degree = 360,
rou1 = 0.1, col = "#4DAF4A", border = "#EEEEEE")
draw.sector(center = c(0, 0), start.degree = 0, end.degree = 360,
rou1 = 0.05, col = "#E41A1C", border = "#EEEEEE")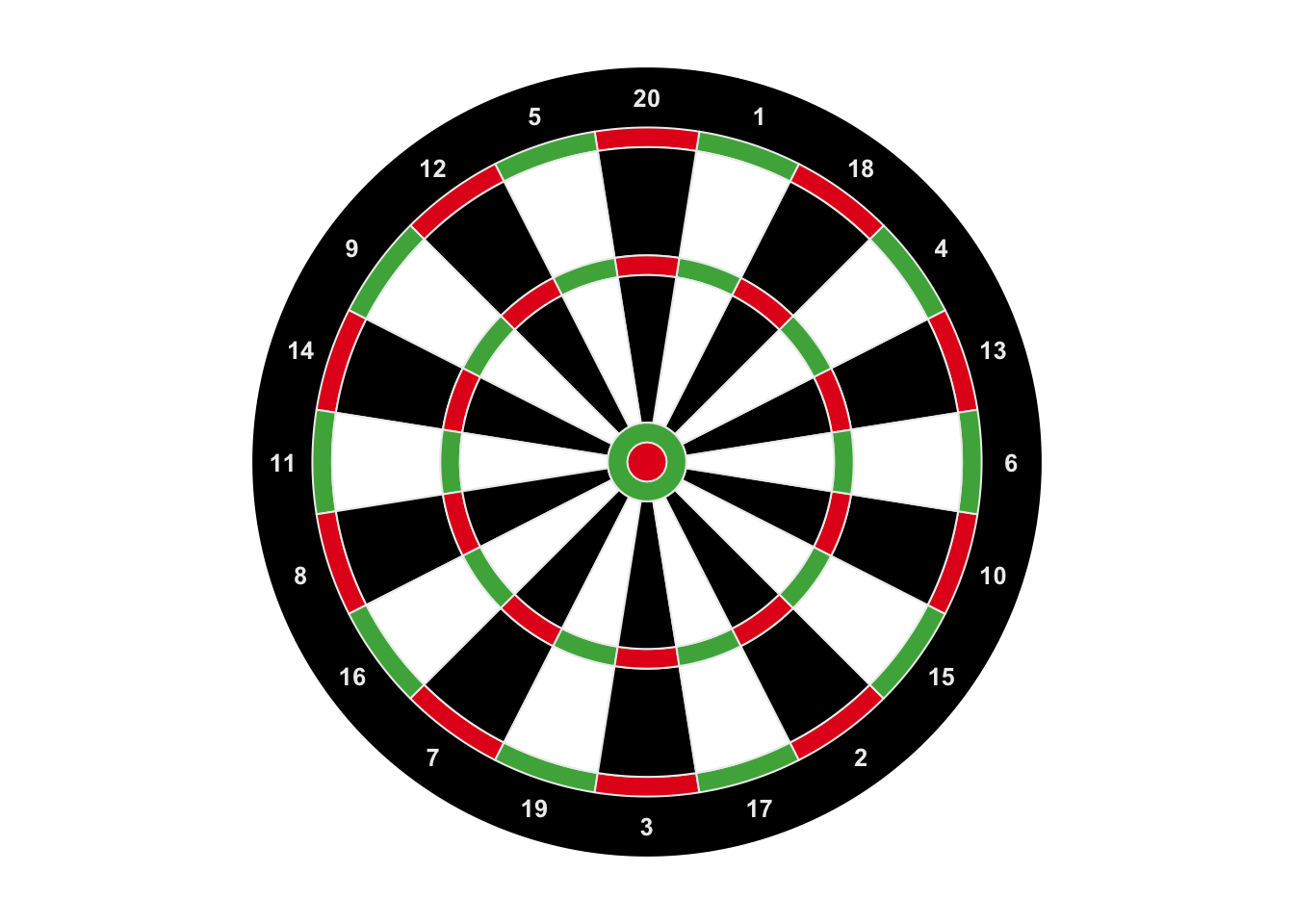
Figure 17.2: A dartboard.
circos.clear()17.3 Ba-Gua and Tai-Ji
The third example is Ba-Gua. The
key functions are circos.rect() and draw.sector() (Figure 17.3).
Bagua was originated several thousands years ago in China. It is the source of almost all ancient Chinese philosophy. It abstracts the rule of universe into base signs and combination of the two basic signs generates the whole system of the universe.
Inside Ba-Gua, these is the Tai-Ji. Tai-Ji refers to the most original state at the creation of the universe. In ancient Chinese philosophy system, at the very beginning, the whole world is a huge mass of air (chaos). Then the lighter air floated up and created sky while heavier sinked down and created ground. The upper world is called Yang and the bottom world is called Ying. And that is Tai-Ji.
Looking at Tai-Ji, you can see there are two states interacting with each other. The white one and the black one gradually transformed into each other at the end. And in the center of white and black, the opposite color is generated. In real world, Taiji can represent all phenomenon that is of dualism. Such as male and female, correct and wrong. However things would change, good thing would become bad thing as time goes by, and bad thing would also turn into good according to how you look at the world.
sectors = 1:8
circos.par(start.degree = 22.5, gap.degree = 6)
circos.initialize(sectors, xlim = c(0, 1))
# yang yao is __ (a long segment)
add_yang_yao = function() {
circos.rect(0,0,1,1, col = "black")
}
# yin yao is -- (two short segments)
add_yin_yao = function() {
circos.rect(0,0,0.45,1, col = "black")
circos.rect(0.55,0,1,1, col = "black")
}
circos.track(ylim = c(0, 1), sectors = sectors, bg.border = NA,
panel.fun = function(x, y) {
i = get.cell.meta.data("sector.numeric.index")
if(i %in% c(2, 5, 7, 8)) add_yang_yao() else add_yin_yao()
}, track.height = 0.1)
circos.track(ylim = c(0, 1), sectors = sectors, bg.border = NA,
panel.fun = function(x, y) {
i = get.cell.meta.data("sector.numeric.index")
if(i %in% c(1, 6, 7, 8)) add_yang_yao() else add_yin_yao()
}, track.height = 0.1)
circos.track(ylim = c(0, 1), sectors = sectors, bg.border = NA,
panel.fun = function(x, y) {
i = get.cell.meta.data("sector.numeric.index")
if(i %in% c(4, 5, 6, 7)) add_yang_yao() else add_yin_yao()
}, track.height = 0.1)
# the bottom of the most recent track
r = get.cell.meta.data("cell.bottom.radius") - 0.1
# draw taiji, note default order is clock wise for `draw.sector`
draw.sector(center = c(0, 0), start.degree = 90, end.degree = -90,
rou1 = r, col = "black", border = "black")
draw.sector(center = c(0, 0), start.degree = 270, end.degree = 90,
rou1 = r, col = "white", border = "black")
draw.sector(center = c(0, r/2), start.degree = 0, end.degree = 360,
rou1 = r/2, col = "white", border = "white")
draw.sector(center = c(0, -r/2), start.degree = 0, end.degree = 360,
rou1 = r/2, col = "black", border = "black")
draw.sector(center = c(0, r/2), start.degree = 0, end.degree = 360,
rou1 = r/8, col = "black", border = "black")
draw.sector(center = c(0, -r/2), start.degree = 0, end.degree = 360,
rou1 = r/8, col = "white", border = "white")
Figure 17.3: Ba-Gua and Tai-Ji.
circos.clear()