Skip to contents

Topic 2-03: Implement GSEA from scratch

Zuguang Gu

2025-05-31

Source: vignettes/topic2_03_implement_gsea.Rmd
topic2_03_implement_gsea.Rmd

In this document, we will implement the two versions of GSEA in R, using the p53 dataset also from the GSEA 2005 paper.

library(GSEAtopics)
data(p53_dataset)
expr = p53_dataset$expr  # expression matrix
condition = p53_dataset$condition  # experimental labels
gs = p53_dataset$gs  # C2 gene sets

geneset = gs[["p53hypoxiaPathway"]]
geneset = intersect(geneset, rownames(expr))

This gene set is very small:

length(geneset)
## [1] 20

Note, in all other vignettes, we use “MUT” as the treatment and “WT” as the control. But in this vignette, the p53hypoxiaPathway is a perfect example to show the ideas of GSEA, but it is down-regulated in MUT. Thus we change the direction of the comparison to let “WT” be the treatment then the p53hypoxiaPathway gene set has an up-regulation.

condition = factor(condition, levels = c("WT", "MUT"))

The heatmap of genes in this gene set:

library(genefilter)
tdf = rowttests(expr, condition)
tdf$p_adjust = p.adjust(tdf$p.value, "BH")

library(ComplexHeatmap)
Heatmap(t(scale(t(expr[geneset, ]))), 
    column_split = condition, cluster_column_slices = FALSE,
    top_annotation = HeatmapAnnotation(condition = condition),
    right_annotation = rowAnnotation(tvalue = anno_points(tdf[geneset, "statistic"],
                                              gp = gpar(col = ifelse(tdf[geneset, "p.value"] < 0.01, "red", "black")),
                                              width = unit(2, "cm"))))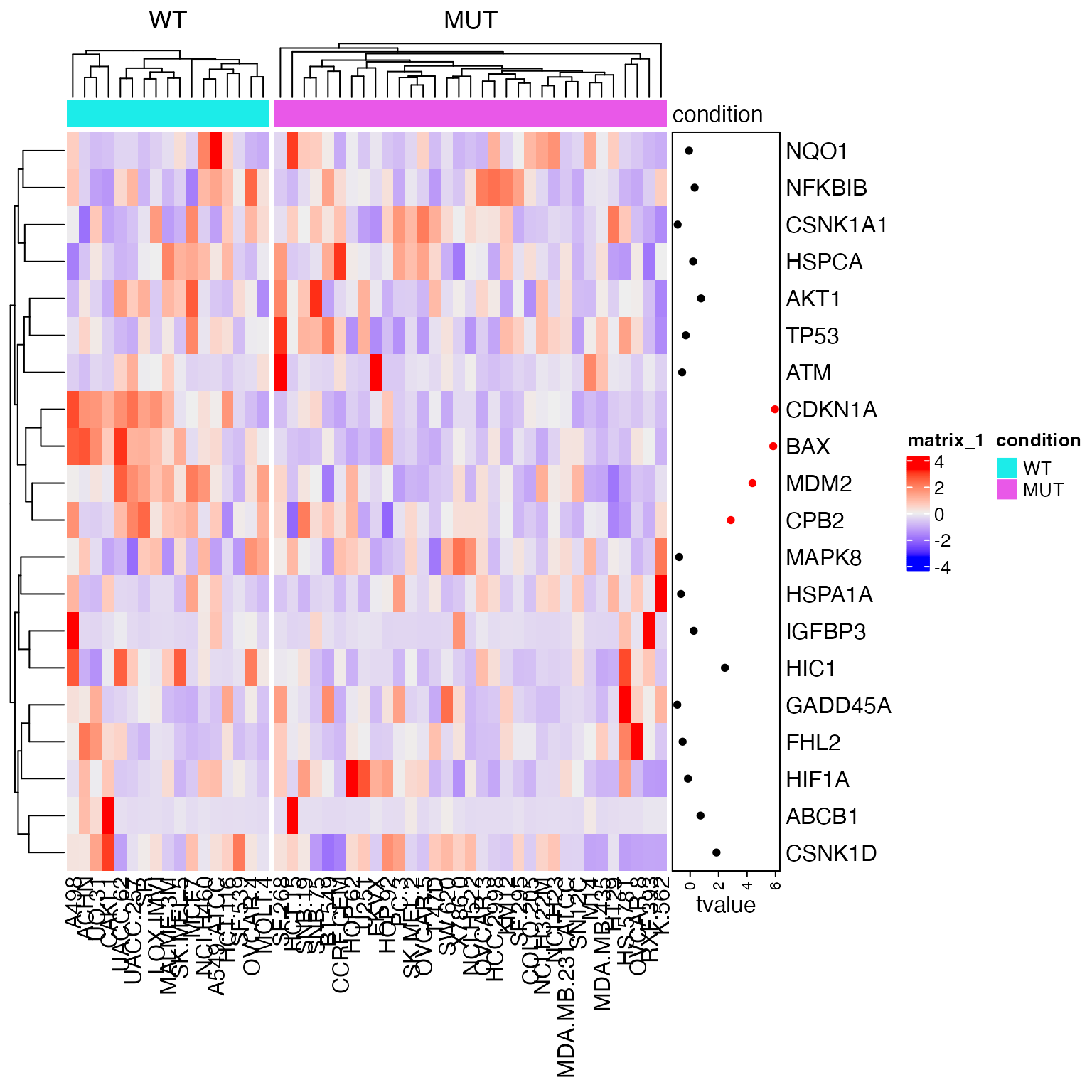

Note here gene IDs in the expression matrix and in the gene set are all gene symbols, thus no more adjustment needs to be done here.

The gene-level difference score is set as signal-to-noise ratios, which is:

μ1−μ2σ1+σ2 \frac{\mu_1 - \mu_2}{\sigma_1 + \sigma_2}

We calculate the gene-level difference score in s:

s = apply(expr, 1, function(x) {
    x1 = x[condition == "WT"]
    x2 = x[condition == "MUT"]
    (mean(x1) - mean(x2))/(sd(x1) + sd(x2))
})

A faster way to calculate s is to use the matrixStats packages.

library(matrixStats)
m1 = expr[, condition == "WT"]  # only samples in group 1
m2 = expr[, condition == "MUT"]  # only samples in group 2
s = (rowMeans(m1) - rowMeans(m2))/(rowSds(m1) + rowSds(m2)) # gene-level difference scores

Sort the gene scores from the highest to the lowest:

s = sort(s, decreasing = TRUE)

For simplicity, we mainly demonstrate the implementation for enrichment of up-regulation (right-sided).

GSEA version 1

Calculate enrichment score

Next we first implement the original GSEA method, which was proposed in Mootha et al. 2003.

We calculate the cummulative probability of a gene being in a gene set GkG_k. At position pp in the sorted gene score vector:

f1p=1nk∑i=1pI(gi∈Gk) f_{1p} = \frac{1}{n_k} \sum_{i=1}^p I(g_i \in G_k) 

## original GSEA
l_set = names(s) %in% geneset
f1 = cumsum(l_set)/sum(l_set)

## or
binary_set = l_set + 0
f1 = cumsum(binary_set)/sum(binary_set)

Here in the calculation of f1, sum(l_set) is nkn_k, cumsum(l_set) is ∑i=1pI(gi∈Gk)\sum_{i=1}^p I(g_i \in G_k).

Similarly, we calculate the cummulative distribution of a gene not in the gene set.

l_other = ! names(s) %in% geneset
f2 = cumsum(l_other)/sum(l_other)

f1 and f2 can be used to plot the CDFs of two distributions.

n = length(s)
plot(1:n, f1, type = "l", col = "red", xlab = "sorted genes")
lines(1:n, f2, col = "blue")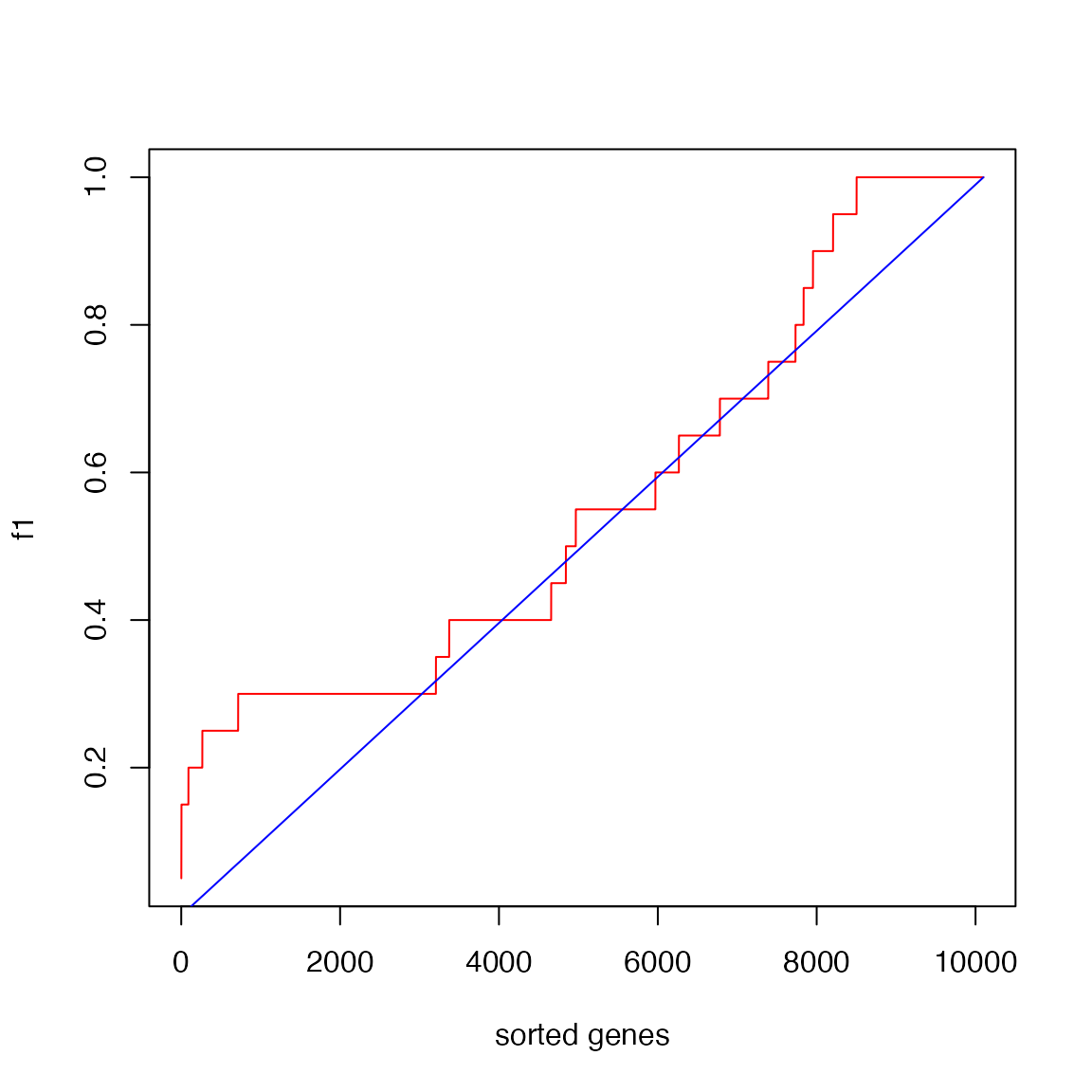

The reason why the blue locates almost on the diagonal is the gene set is very small.

Next the difference of cumulative probability (f1 - f2) at each position on the sorted gene list. Let’s call it “the GSEA plot”.

plot(f1 - f2, type = "l", xlab = "sorted genes")
abline(h = 0, lty = 2, col = "grey")
points(which(l_set), rep(0, sum(l_set)), pch = "|", col = "red")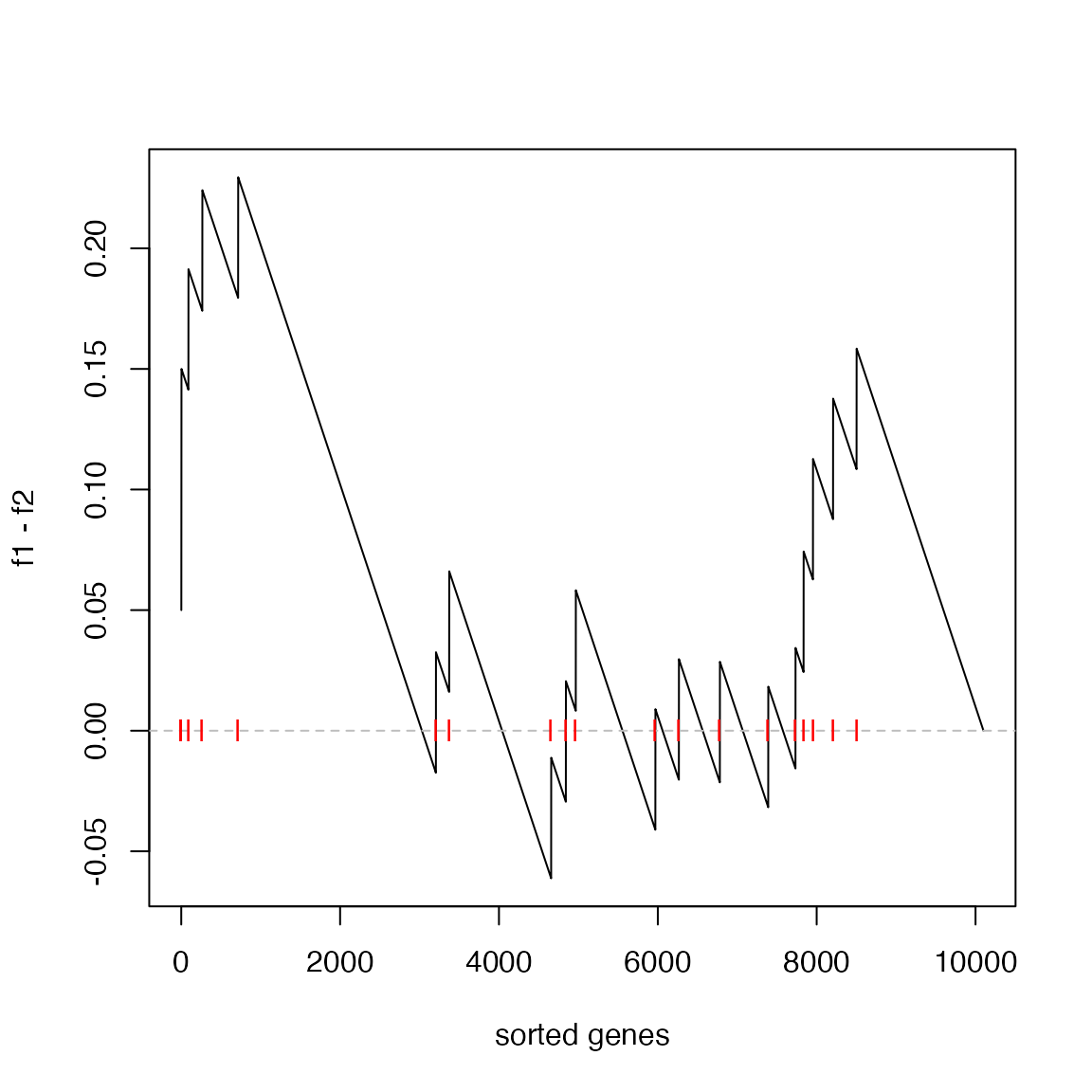

The enrichment score (ES) defined as max(f1 - f2) is:

es = max(f1 - f2)
es
## [1] 0.2294643

And the position in the “GSEA plot”:

plot(f1 - f2, type = "l", xlab = "sorted genes")
abline(h = 0, lty = 2, col = "grey")
points(which(l_set), rep(0, sum(l_set)), pch = "|", col = "red")
abline(v = which.max(f1 - f2), lty = 3, col = "blue")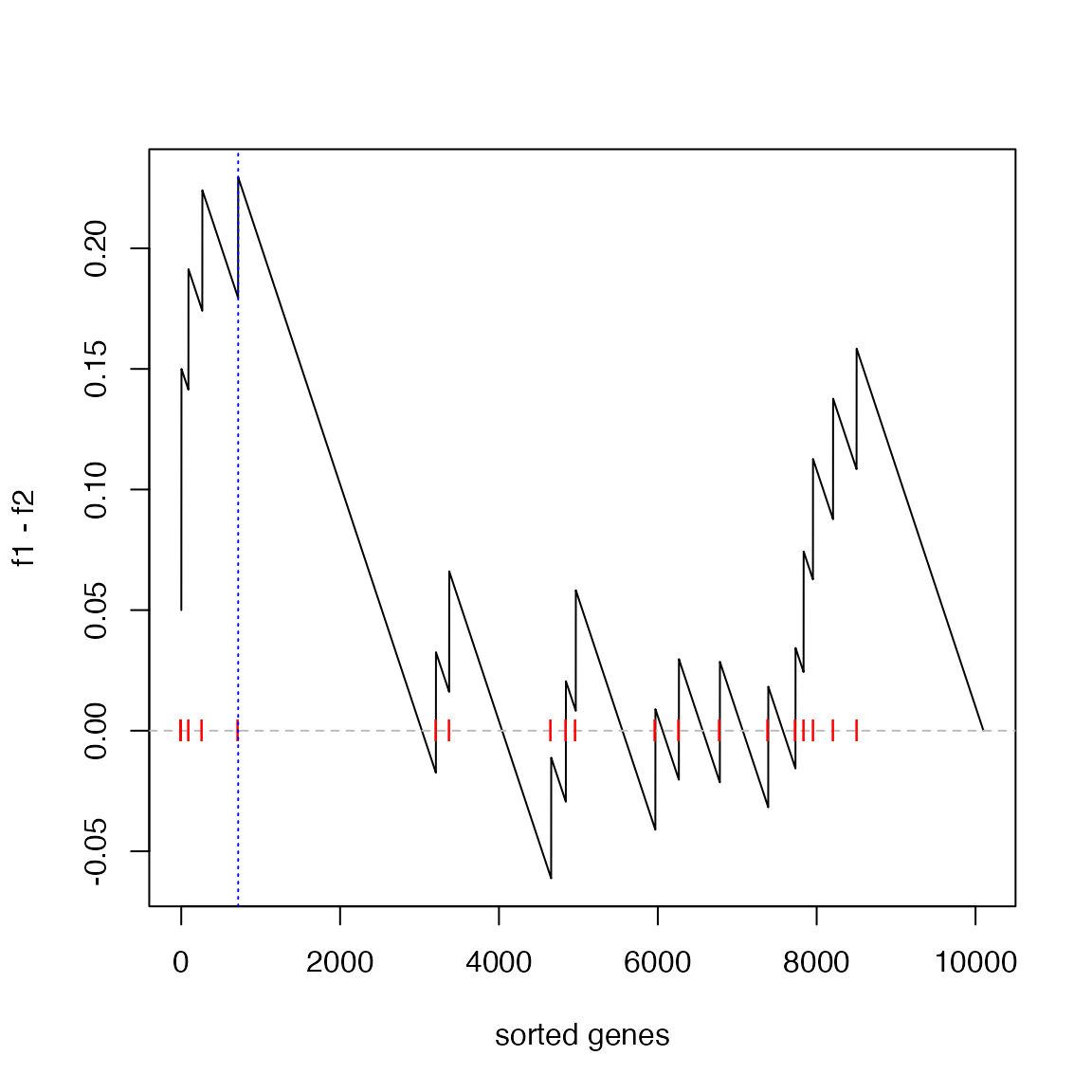

The statistic es actually is the Kolmogorov-Smirnov statistics, thus, we can directly apply the KS test where the two vectors for the KS test are the positions on the sorted gene list.

ks.test(which(l_set), which(l_other))
## 
##  Asymptotic two-sample Kolmogorov-Smirnov test
## 
## data:  which(l_set) and which(l_other)
## D = 0.22946, p-value = 0.244
## alternative hypothesis: two-sided

However, we can see the p-value is not significant for this gene set. This is because KS test is not a powerful test. Next we construct the null distribution by sample permutation.

Sample permutation

In the next code chunk, the calculation of ES score is wrapped into a function, also we use rowMeans() and rowSds() to speed up the calculation of gene-level scores.

library(matrixStats)
# expr: the complete expression matrix
# condition: the condition labels of samples, level[1] > level[2] means up-regulation
# geneset: A vector of genes
condition = factor(condition, level = c("WT", "MUT"))
calculate_es = function(expr, condition, geneset) {

    cmp = levels(condition)

    m1 = expr[, condition == cmp[1]]  # only samples in group 1
    m2 = expr[, condition == cmp[2]]  # only samples in group 2

    s = (rowMeans(m1) - rowMeans(m2))/(rowSds(m1) + rowSds(m2)) # a gene-level difference socre (S2N ratio) 

    s = sort(s, decreasing = TRUE)  # ranked gene list

    l_set = names(s) %in% geneset
    f1 = cumsum(l_set)/sum(l_set)   # CDF for genes in the set

    l_other = !l_set
    f2 = cumsum(l_other)/sum(l_other)  # CDF for genes not in the set

    max(f1 - f2)
}

The ES score calculated by calculate_es():

es = calculate_es(expr, condition, geneset)
es
## [1] 0.2294643

We randomly permute sample labels or we randomly permute condition. These two ways are identical. The aim is to break the association between condition and expr.

condition_random = sample(condition)
expr = expr[, sample(ncol(expr))]

We do sample permutation 1000 times. The random ES scores are saved in es_rand.

set.seed(123)
es_rand = numeric(1000)
for(i in 1:1000) {
    es_rand[i] = calculate_es(expr, sample(condition), geneset)
}

p-value is calculated as the proportion of values in es_rand being equal to or larger than es.

sum(es_rand >= es)/1000
## [1] 0.129

The null distribution of ES:

hist(es_rand)
abline(v = es, col = "red")

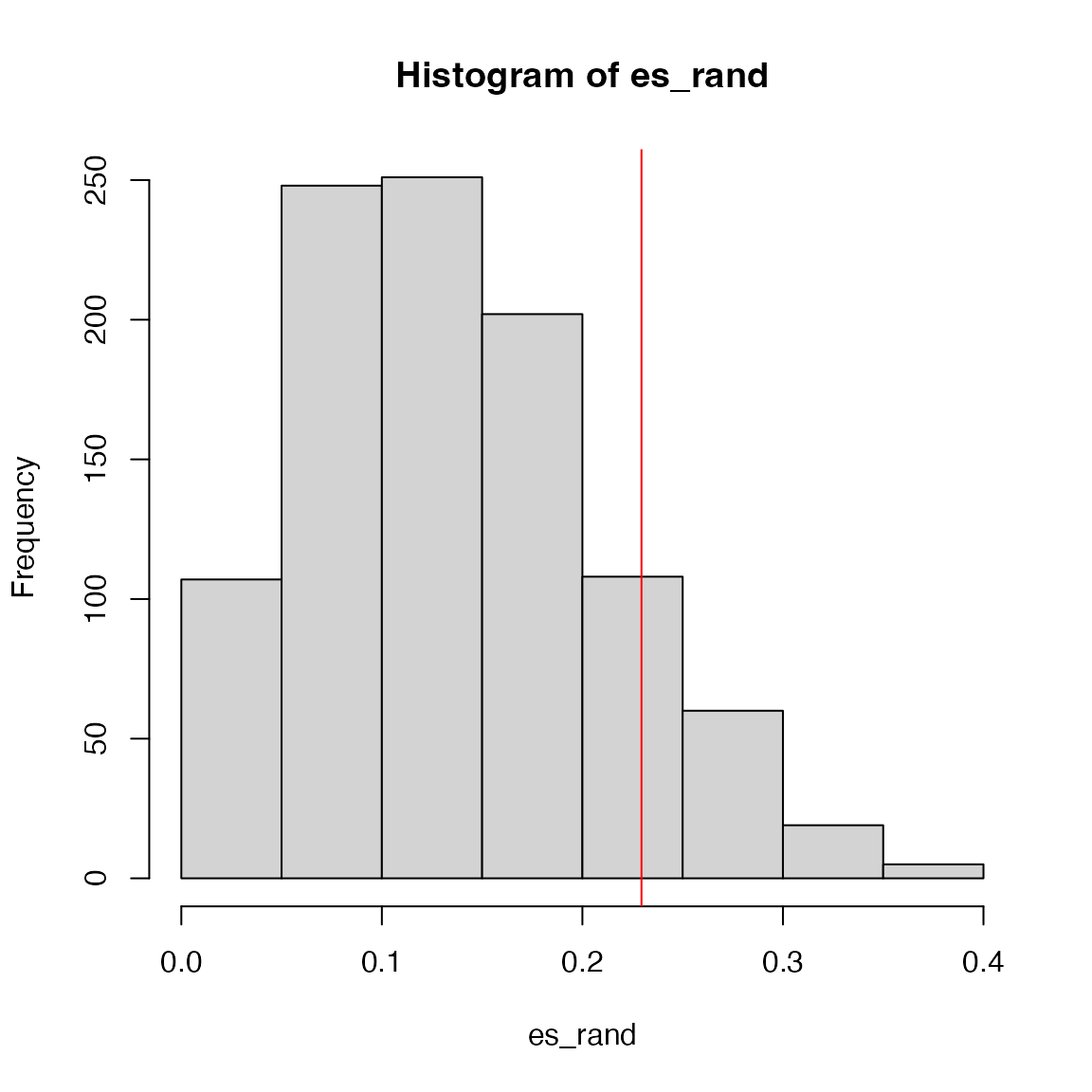
GSEA version 2

Next we implement the improved GSEA (Subramanian et al., PNAS, 2005) where gene-level scores are taken as the weights. The CDF of genes in the gene set is adjusted to:

f1p=1S∑i=1pI(gi∈Gk)⋅|ti|a f_{1p} = \frac{1}{S} \sum_{i=1}^p I(g_i \in G_k)\cdot |t_i|^a

where

S=∑i=1NI(gi∈Gk)⋅|ti|a S = \sum_{i=1}^{N} I(g_i \in G_k)\cdot |t_i|^a

aa is the power of the weight and NN is the total number of genes in the experiment.

We directly modify calculate_es() to calculate_es_v2() where there is only two lines new, which we highlight in the code chunk:

calculate_es_v2 = function(expr, condition, geneset, plot = FALSE, power = 1) {

    cmp = levels(condition)

    m1 = expr[, condition == cmp[1]]
    m2 = expr[, condition == cmp[2]]

    s = (rowMeans(m1) - rowMeans(m2))/(rowSds(m1) + rowSds(m2))

    s = sort(s, decreasing = TRUE)

    l_set = names(s) %in% geneset
    
    # f1 = cumsum(l_set)/sum(l_set)  # <<-- the original line
    
    s_set = abs(s)^power   # <<-- here
    s_set[!l_set] = 0
    f1 = cumsum(s_set)/sum(s_set)  ## <<- here

    l_other = !l_set
    f2 = cumsum(l_other)/sum(l_other)

    if(plot) {
        plot(f1 - f2, type = "l", xlab = "sorted genes")
        abline(h = 0, lty = 2, col = "grey")
        points(which(l_set), rep(0, sum(l_set)), pch = "|", col = "red")
        abline(v = which.max(f1 - f2), lty = 3, col = "blue")
    }

    max(f1 - f2)
}

Now we calculate the new ES score and make the GSEA plot:

es = calculate_es_v2(expr, condition, geneset, plot = TRUE)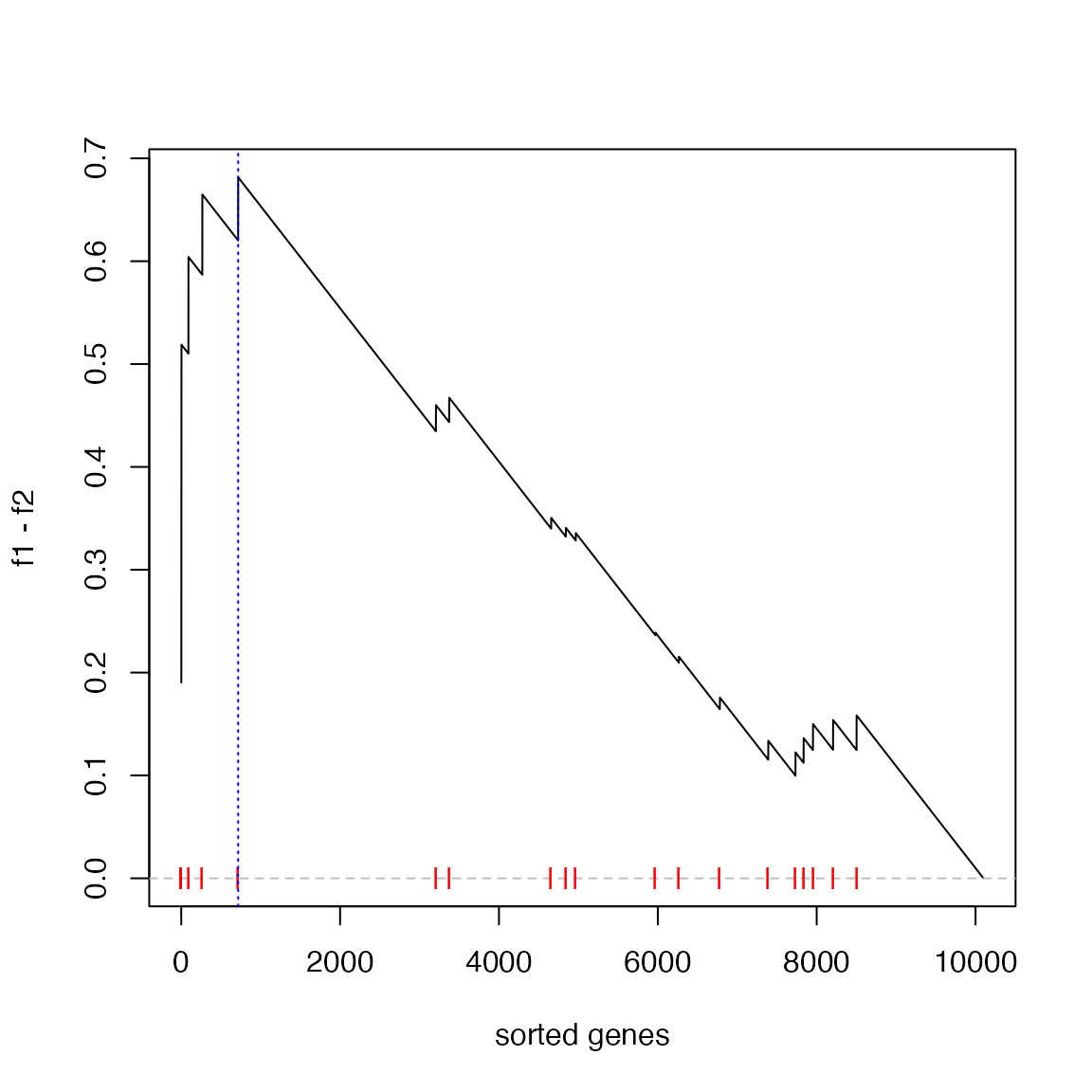

We can also check when power = 0 and power = 2:

par(mfrow = c(1, 2))
calculate_es_v2(expr, condition, geneset, plot = TRUE, power = 0)  # same as the original GSEA
## [1] 0.2294643
title("power = 0")

calculate_es_v2(expr, condition, geneset, plot = TRUE, power = 2)
## [1] 0.8925371
title("power = 2")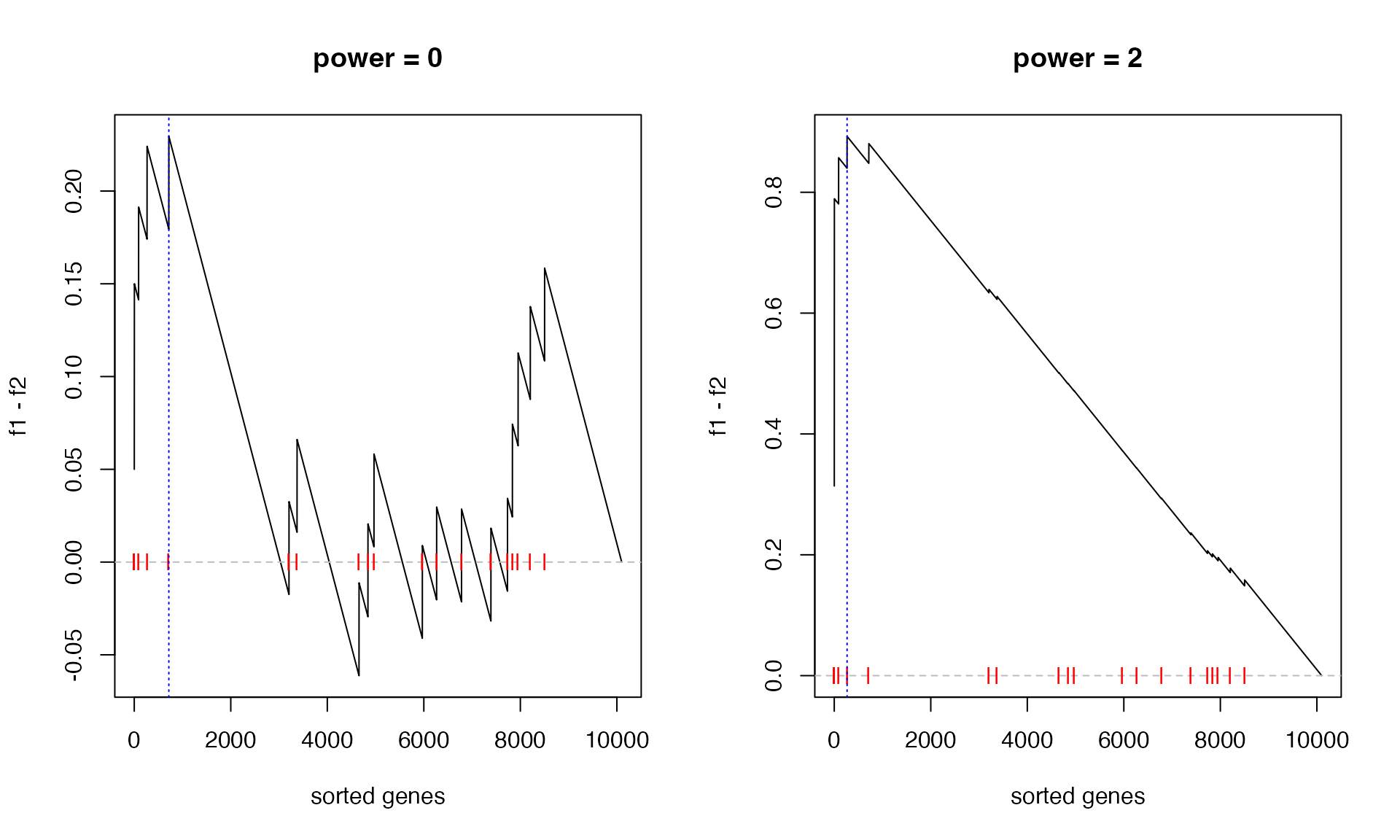

Similarly, we randomly permute samples to obtain the null distribution of ES:

es_rand = numeric(1000)
for(i in 1:1000) {
    es_rand[i] = calculate_es_v2(expr, sample(condition), geneset)
}

The new p-value:

sum(es_rand >= es)/1000
## [1] 0

The minimal p-value from 1000 permutations is 1/1000, so zeor here means p-value < 0.001.

And the null distribution of ES:

hist(es_rand, xlim = c(0, 1))
abline(v = es, col = "red")

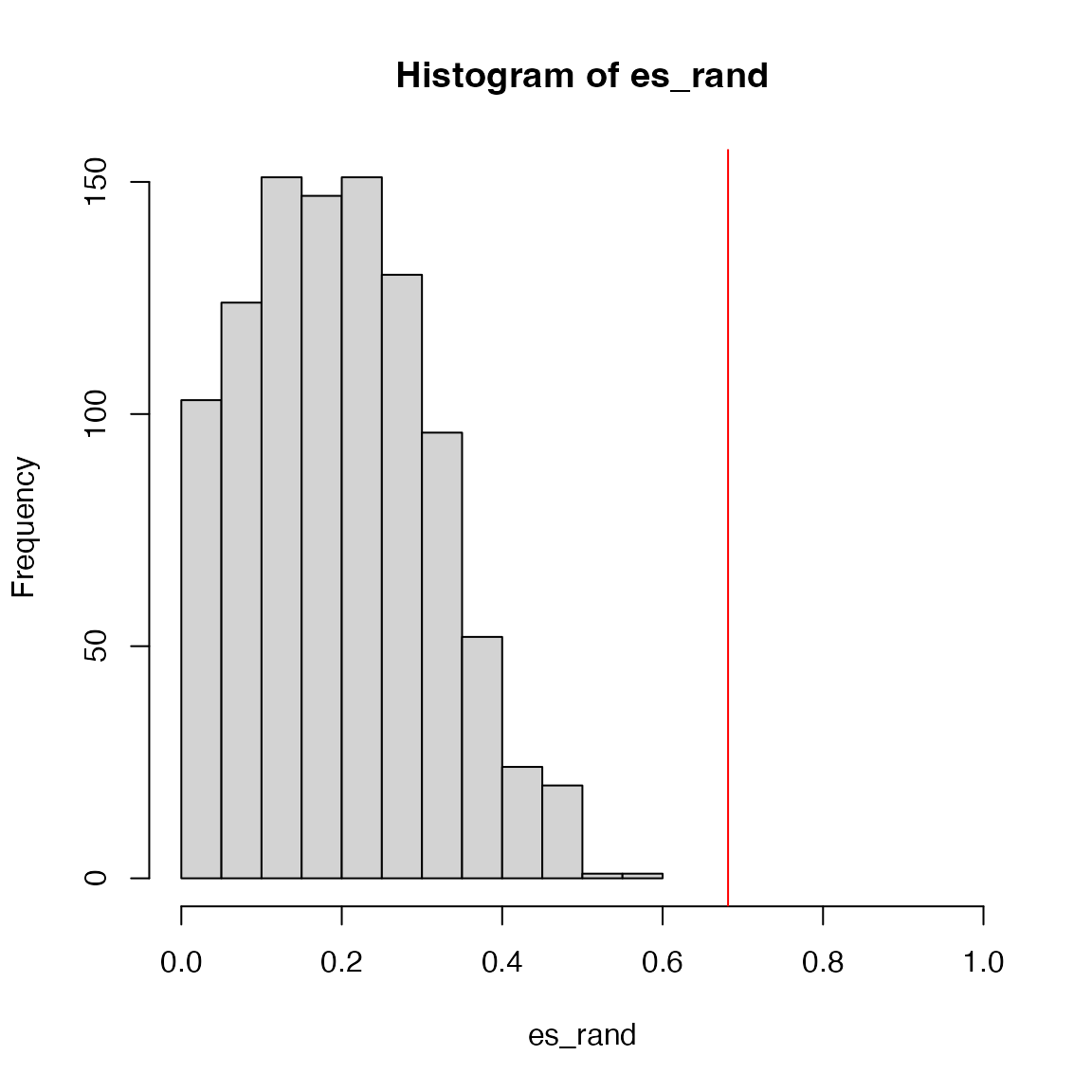
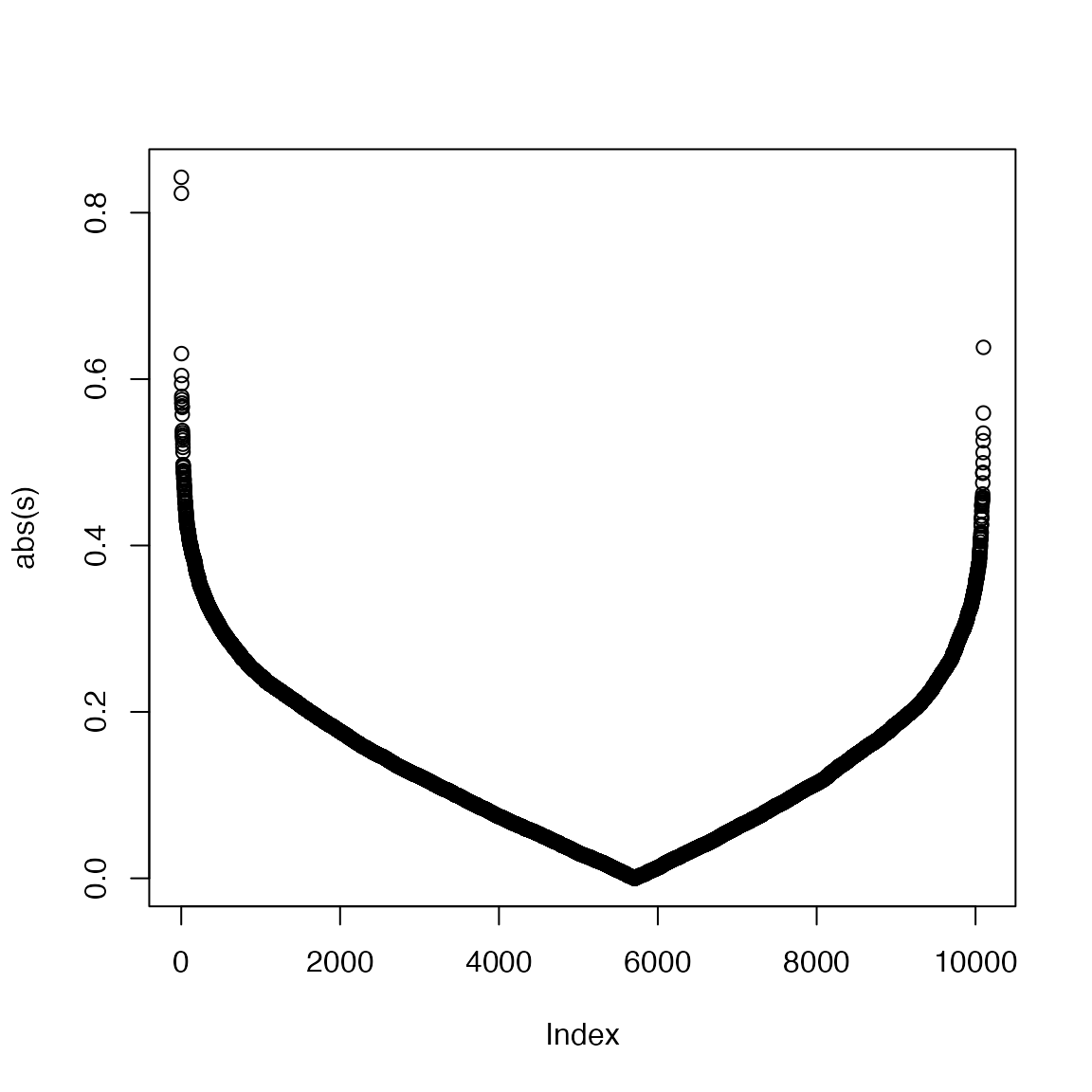
We can see the improved GSEA is more powerful than the original GSEA, because the original GSEA equally weights genes and the improved GSEA weights genes based on their differential expression, which increases the effect of diff genes. Let’s plot the weight of genes:

plot(abs(s))

GSEA version 2, gene permutation

Null distribution can also be constructed by gene permutation. It is very easy to implement:

# s: a vector of pre-calcualted gene-level scores
# s should be sorted
calculate_es_v2_gene_perm = function(s, geneset, perm = FALSE, plot = FALSE, power = 1) {
    
    if(perm) {
        # s is still sorted, but the gene labels are randomly shuffled
        # to break the associations between gene scores and gene labels.
        # also s is still sorted
        names(s) = sample(names(s))  ## <<- here
    }

    l_set = names(s) %in% geneset
    s_set = abs(s)^power
    s_set[!l_set] = 0
    f1 = cumsum(s_set)/sum(s_set)

    l_other = !l_set
    f2 = cumsum(l_other)/sum(l_other)

    if(plot) {
        plot(f1 - f2, type = "l", xlab = "sorted genes")
        abline(h = 0, lty = 2, col = "grey")
        points(which(l_set), rep(0, sum(l_set)), pch = "|", col = "red")
        abline(v = which.max(f1 - f2), lty = 3, col = "blue")
    }

    max(f1 - f2)
}

Good thing of gene permutation is the gene-level scores only need to be calculated once and can be repeatedly used.

# pre-calculate gene-level scores
m1 = expr[, condition == "WT"]
m2 = expr[, condition == "MUT"]

s = (rowMeans(m1) - rowMeans(m2))/(rowSds(m1) + rowSds(m2))
s = sort(s, decreasing = TRUE)  # must be pre-sorted

The GSEA plot under gene permutation:

es = calculate_es_v2_gene_perm(s, geneset, plot = TRUE)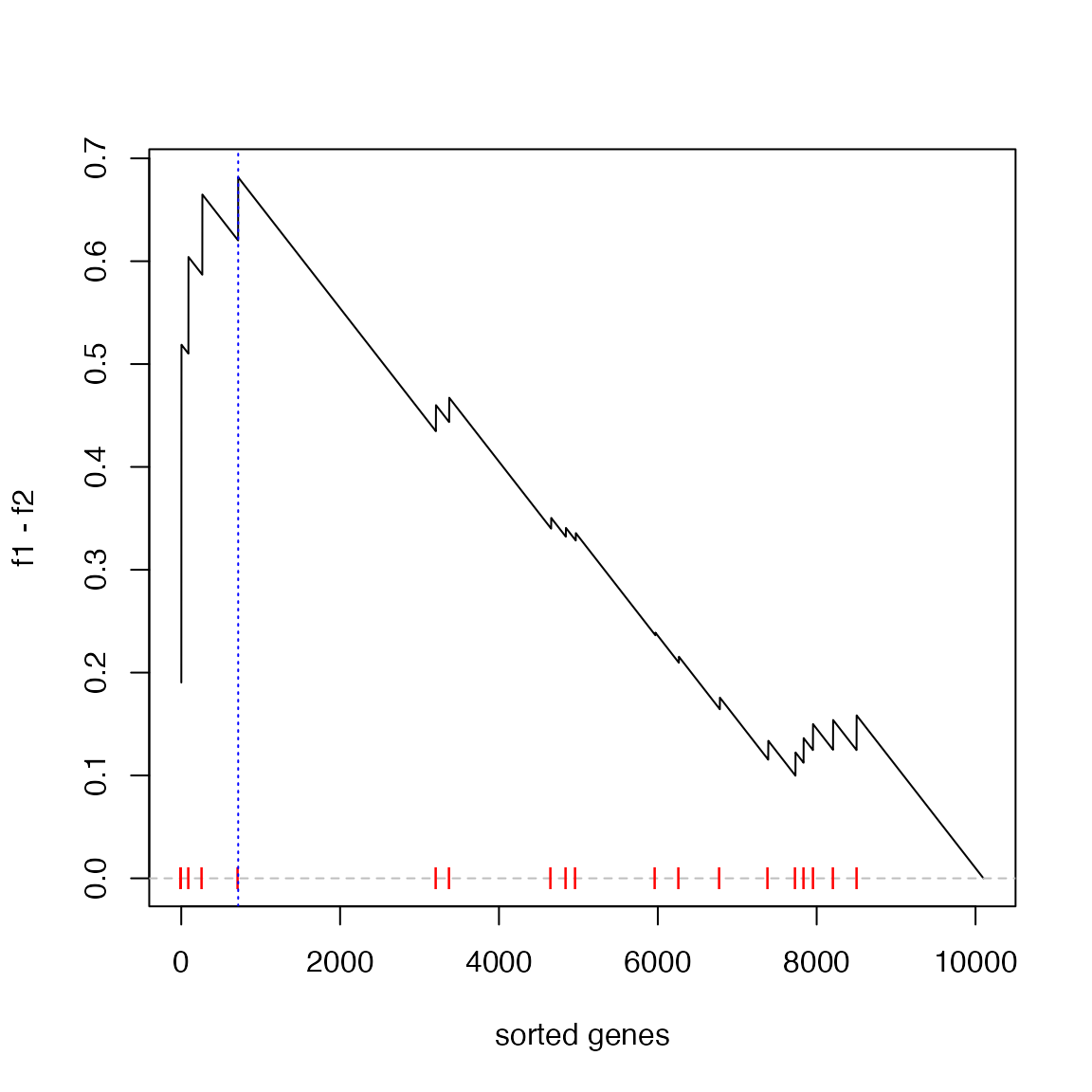

We calculate the null distribution of ES from gene permutation:

es_rand = numeric(1000)
for(i in 1:1000) {
    es_rand[i] = calculate_es_v2_gene_perm(s, geneset, perm = TRUE)
}

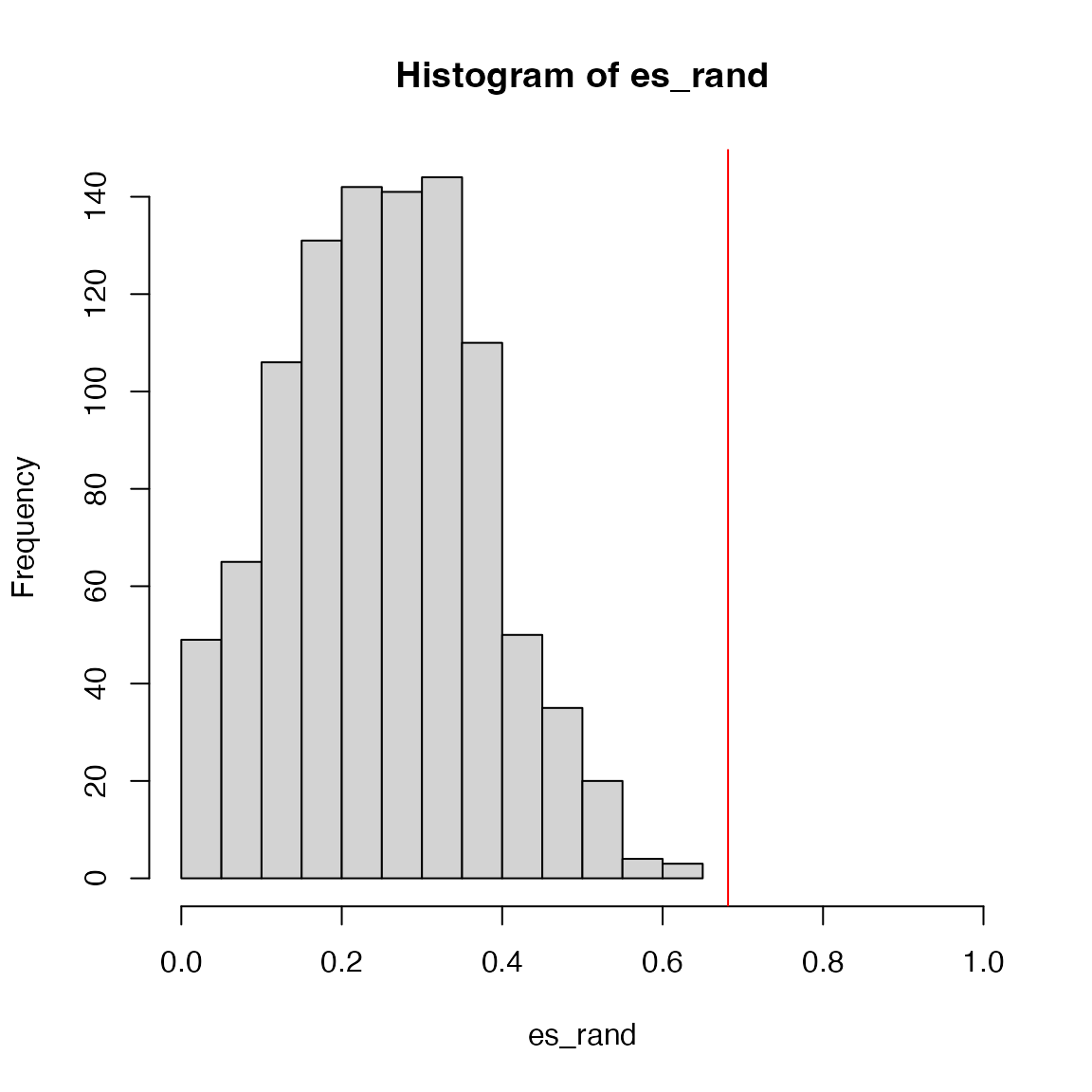
sum(es_rand >= es)/1000
## [1] 0

The real p-value is also < 0.001.

The null distribution of ES from gene permutation:

hist(es_rand, xlim = c(0, 1))
abline(v = es, col = "red")

Other statistics

Taking es and es_rand calculated previously, NES is calculated as

es/mean(es_rand)
## [1] 2.692013

NES does not take into account of the dispersion of es_rand, sometimes z-scores is used instead:

(es - mean(es_rand))/sd(es_rand)
## [1] 3.483993

Two-sided test

The ES score we have introduced is one-sided (right-sided), i.e. we only look at the enrichment for up-regulated genes. Basically, if there exist negative values in f2 - f1, it means there is also an enrichment for down-regulated genes. There are two ways to obtain a statistics for two-sided test:

  1. max(|ES+|,|ES−|)⋅sign(max)\max( |\mathrm{ES}^+|, |\mathrm{ES}^-|) \cdot \mathrm{sign}(\mathrm{max})
  2. |ES+|−|ES−||\mathrm{ES}^+| - |\mathrm{ES}^-|

where ES+=max(f2−f1)\mathrm{ES}^+ = \max(f_2 - f_1), ES−=min(f2−f1)\mathrm{ES}^- = \min(f_2 - f_1) and there should exist both positive and negative values in f2−f1f_2 - f_1.

If there are only positive values in f2−f1f_2 - f_1, then the statistic is max(f2−f1)\max(f_2 - f_1), and if there are only negative values in f2−f1f_2 - f_1, the statistic is min(f2−f1)\min(f_2 - f_1).

Standard GSEA uses the first method, i.e. maximal deviation of f2f_2 and f1f_1.

calculate_es_v2_gene_perm_two_sided = function(s, geneset, perm = FALSE, 
    plot = FALSE, power = 1, method = "std") {
    
    if(perm) {
        # s is still sorted, but the gene labels are randomly shuffled
        # to break the associations between gene scores and gene labels.
        names(s) = sample(names(s))  ## <<- here
    }

    l_set = names(s) %in% geneset
    s_set = abs(s)^power
    s_set[!l_set] = 0
    f1 = cumsum(s_set)/sum(s_set)

    l_other = !l_set
    f2 = cumsum(l_other)/sum(l_other)

    m1 = max(f1 - f2)
    m2 = min(f1 - f2)

    if(method == "std") {
        max(m1, -m2)*ifelse(m1 > -m2, sign(m1), sign(m2))
    } else if(method == "diff") {
        if(m1 >= 0 && m2 >= 0) {
            m1
        } else if(m1 <= 0 && m2 <= 0) {
            m2
        } else {
            m1 + m2
        }
    }
}

Random distribution is generated in the same way.

es = calculate_es_v2_gene_perm_two_sided(s, geneset)
es_rand = numeric(1000)
for(i in 1:1000) {
    es_rand[i] = calculate_es_v2_gene_perm_two_sided(s, geneset, perm = TRUE)
}

The calculation of the p-value is a little bit different. For the standard GSEA two-sided method, as ES is actually from two different ES scores, the null distribution is bimodal. If ES is positive, then the p-value as well as NES are only calculated from the right distribution, and if ES is negative, the p-value as well as NES are only calculated from the left distribution (left-sided).

hist(es_rand)
abline(v = es, col = "red")

sum(es_rand > es)/sum(es_rand > 0) # p-value
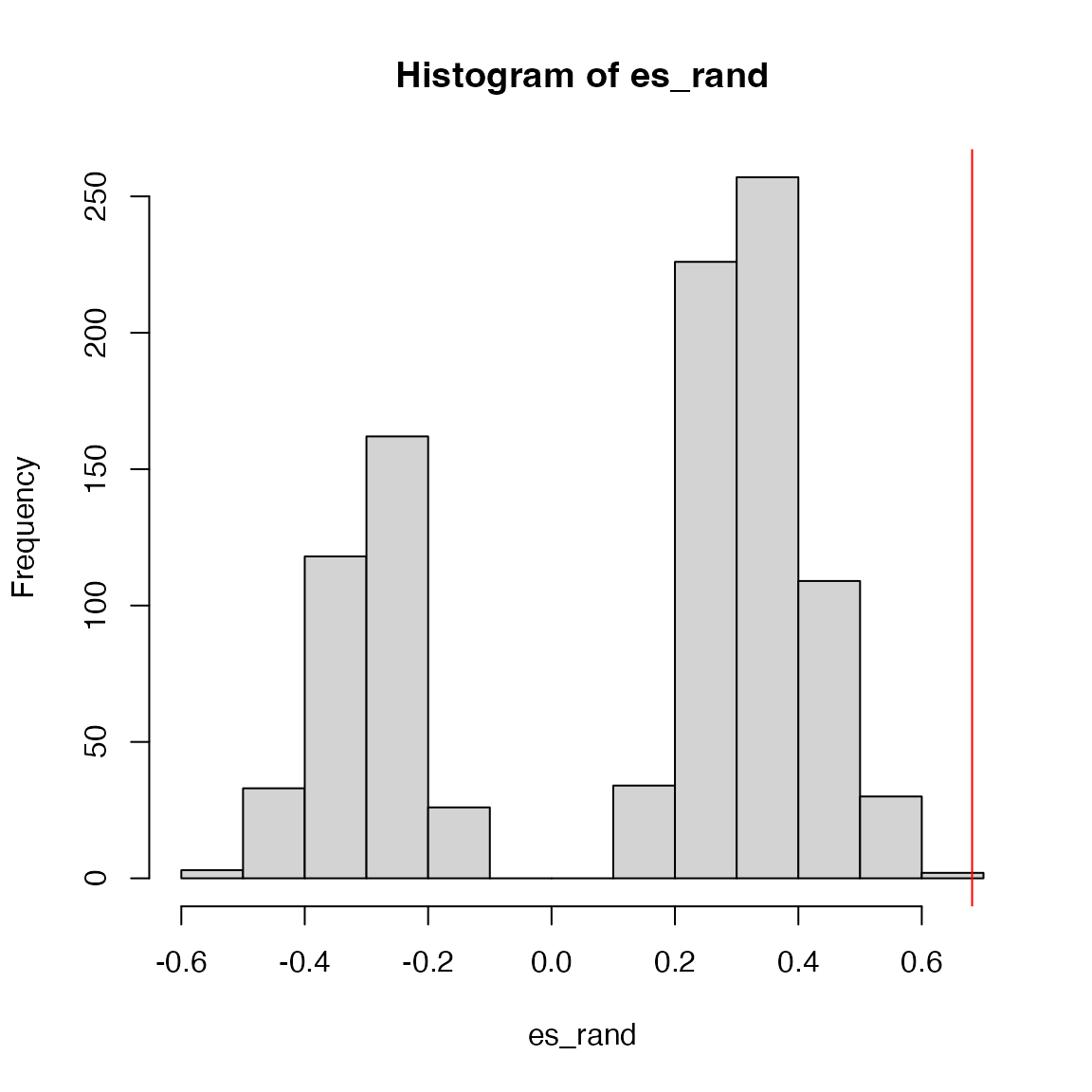
## [1] 0.001519757
es/mean(es_rand[es_rand > es])     # NES
## [1] 0.9784004

For the second method, the null distribution is bell-like.

es = calculate_es_v2_gene_perm_two_sided(s, geneset, method = "diff")
es_rand = numeric(1000)
for(i in 1:1000) {
    es_rand[i] = calculate_es_v2_gene_perm_two_sided(s, geneset, perm = TRUE, method = "diff")
}
hist(es_rand)
abline(v = es, col = "red")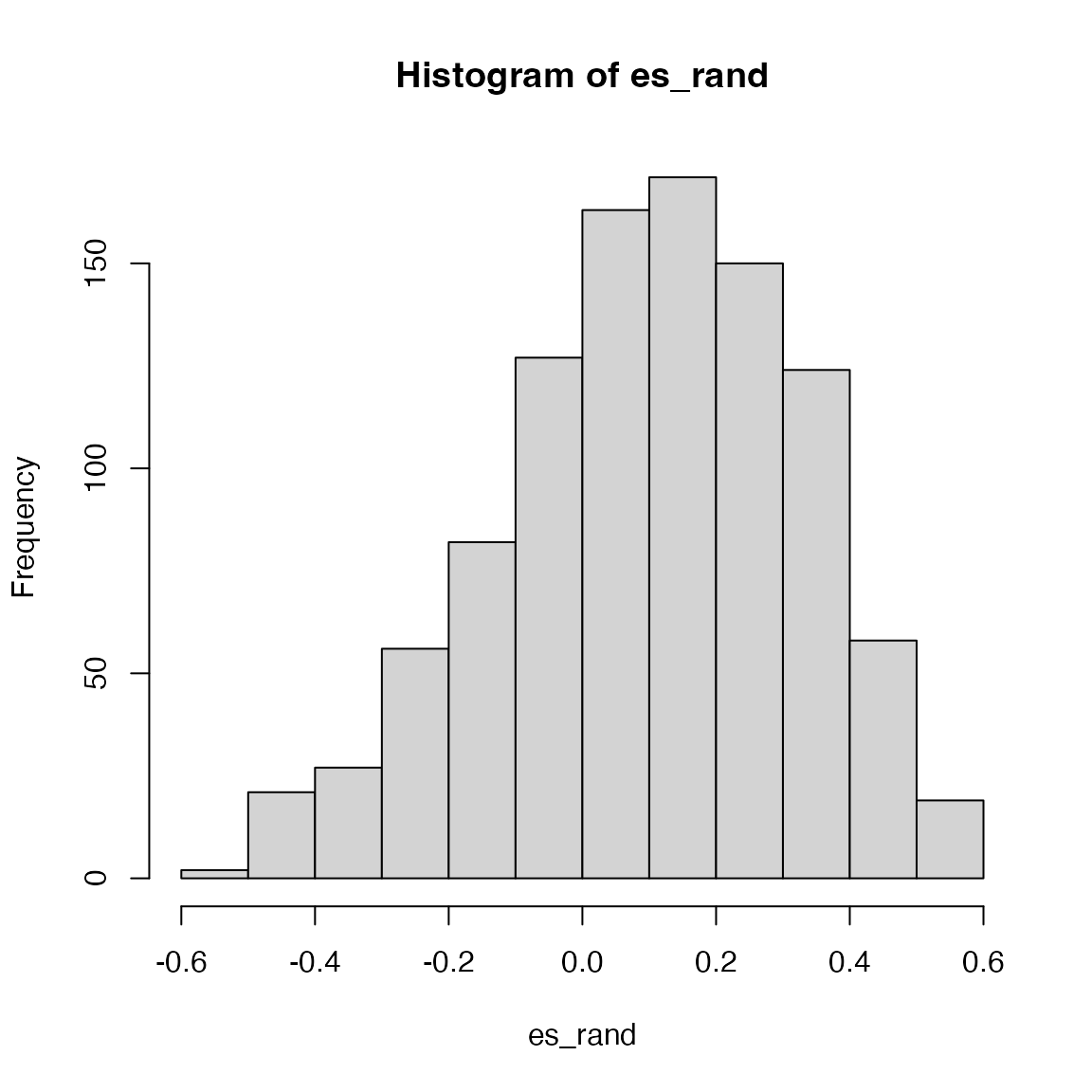

p-value can be calculated as right-sided or left-sided according to the sign of ES, or calculated as sum(abs(es_rand) > abs(es))/perm. For this method, to scale all ES, NES can be defined as a z-score (es-mean(es_rand))/sd(es_rand).

Practice

Practice 1

We have demonstrated two different ways (sample permutation and gene permutation) for calculating p-values. Apply the p53 dataset on the 50 hallmark gene sets, and compare the two enrichment results (e.g. to check which method tends to generate more signficant p-values).

The code we saw so far only applies to a single gene set, you may need to put it into a for loop to go over each of the 50 hallmark gene sets.

The Hallmark gene sets from MSigDB

library(GSEAtopics)
gs_hallmark = get_msigdb(version = "2023.2.Hs", collection = "h.all", gene_id_type = "symbol")
n_gs = length(gs_hallmark)

Sample permutation:

p1 = numeric(n_gs)
es1 = numeric(n_gs)
nes1 = numeric(n_gs)
z1 = numeric(n_gs)

for(i in 1:n_gs) {
    print(i)
    geneset = gs_hallmark[[i]]

    es1[i] = calculate_es_v2(expr, condition, geneset)

    es_rand = numeric(1000)
    for(k in 1:1000) {
        es_rand[k] = calculate_es_v2(expr, sample(condition), geneset = geneset)
    }
    p1[i] = sum(es_rand >= es1[i])/1000
    nes1[i] = es1[i]/mean(es_rand)
    z1[i] = (es1[i] - mean(es_rand))/sd(es_rand)
}
## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5
## [1] 6
## [1] 7
## [1] 8
## [1] 9
## [1] 10
## [1] 11
## [1] 12
## [1] 13
## [1] 14
## [1] 15
## [1] 16
## [1] 17
## [1] 18
## [1] 19
## [1] 20
## [1] 21
## [1] 22
## [1] 23
## [1] 24
## [1] 25
## [1] 26
## [1] 27
## [1] 28
## [1] 29
## [1] 30
## [1] 31
## [1] 32
## [1] 33
## [1] 34
## [1] 35
## [1] 36
## [1] 37
## [1] 38
## [1] 39
## [1] 40
## [1] 41
## [1] 42
## [1] 43
## [1] 44
## [1] 45
## [1] 46
## [1] 47
## [1] 48
## [1] 49
## [1] 50
df1 = data.frame(
    geneset = names(gs_hallmark),
    es = es1,
    nes = nes1,
    z = z1,
    p_value = p1
)

Gene permutation:

m1 = expr[, condition == "WT"]
m2 = expr[, condition == "MUT"]

s = (rowMeans(m1) - rowMeans(m2))/(rowSds(m1) + rowSds(m2))
s = sort(s, decreasing = TRUE)  # must be pre-sorted

p2 = numeric(n_gs)
es2 = numeric(n_gs)
nes2 = numeric(n_gs)
z2 = numeric(n_gs)

for(i in 1:n_gs) {
    print(i)
    geneset = gs_hallmark[[i]]

    es2[i] = calculate_es_v2_gene_perm(s, geneset = geneset)
    
    es_rand = numeric(1000)
    for(k in 1:1000) {
        es_rand[k] = calculate_es_v2_gene_perm(s, geneset = geneset, perm = TRUE)
    }
    p2[i] = sum(es_rand >= es2[i])/1000
    nes2[i] = es2[i]/mean(es_rand)
    z2[i] = (es2[i] - mean(es_rand))/sd(es_rand)
}
## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5
## [1] 6
## [1] 7
## [1] 8
## [1] 9
## [1] 10
## [1] 11
## [1] 12
## [1] 13
## [1] 14
## [1] 15
## [1] 16
## [1] 17
## [1] 18
## [1] 19
## [1] 20
## [1] 21
## [1] 22
## [1] 23
## [1] 24
## [1] 25
## [1] 26
## [1] 27
## [1] 28
## [1] 29
## [1] 30
## [1] 31
## [1] 32
## [1] 33
## [1] 34
## [1] 35
## [1] 36
## [1] 37
## [1] 38
## [1] 39
## [1] 40
## [1] 41
## [1] 42
## [1] 43
## [1] 44
## [1] 45
## [1] 46
## [1] 47
## [1] 48
## [1] 49
## [1] 50
df2 = data.frame(
    geneset = names(gs_hallmark),
    es = es2,
    nes = nes2,
    z = z2,
    p_value = p2
)

Compare ES, NES, z-scores, and p-values:

par(mfrow = c(2, 2))
plot(df1$es, df2$es, main = "ES",
    xlab = "sample permutation", ylab = "gene permutation")
plot(df1$nes, df2$nes, main = "NES", xlim = c(0, 2.5), ylim = c(0, 2.5),
    xlab = "sample permutation", ylab = "gene permutation")
plot(df1$z, df2$z, main = "Z-score",
    xlab = "sample permutation", ylab = "gene permutation")
plot(df1$p_value, df2$p_value, main = "P-value",
    xlab = "sample permutation", ylab = "gene permutation")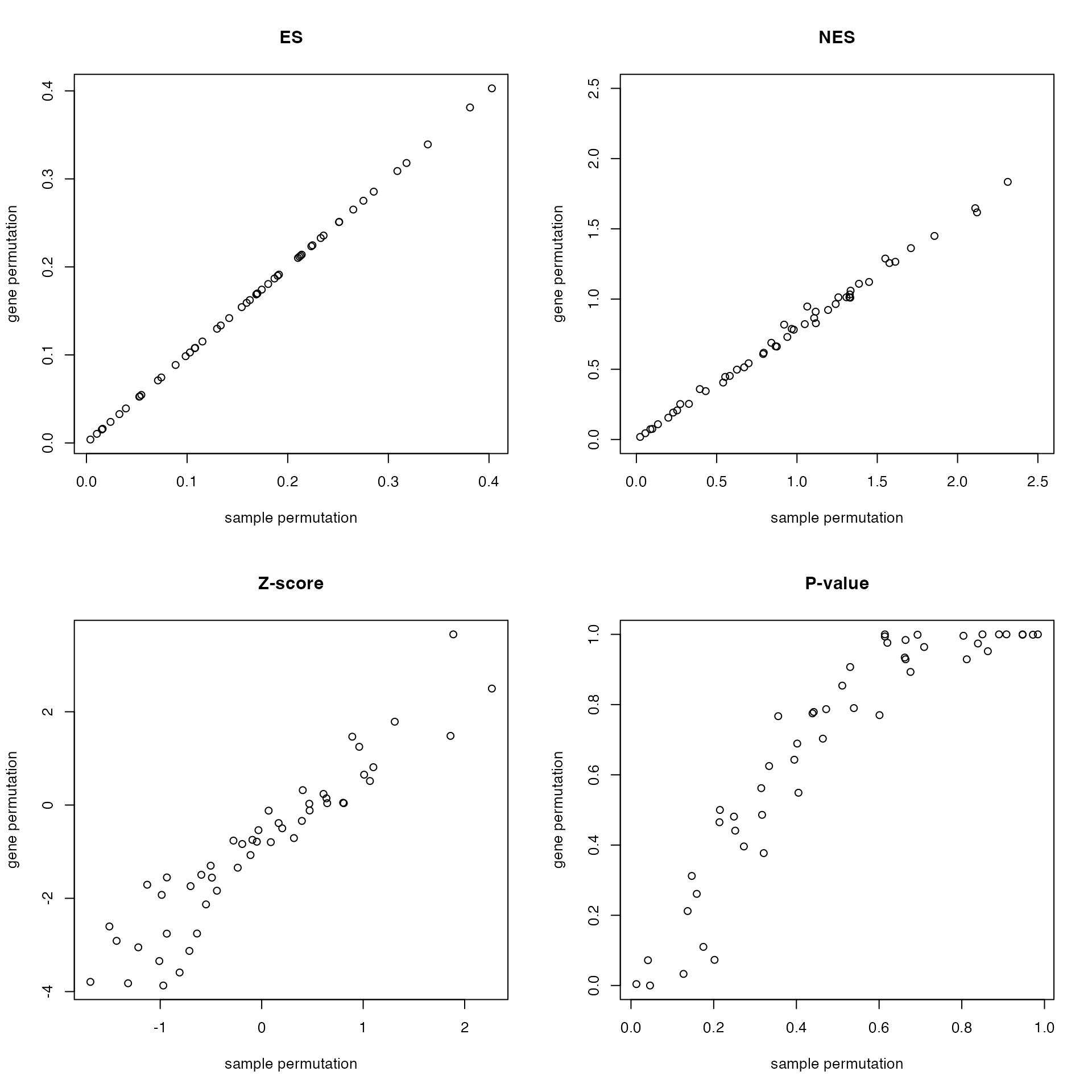

Practice 2

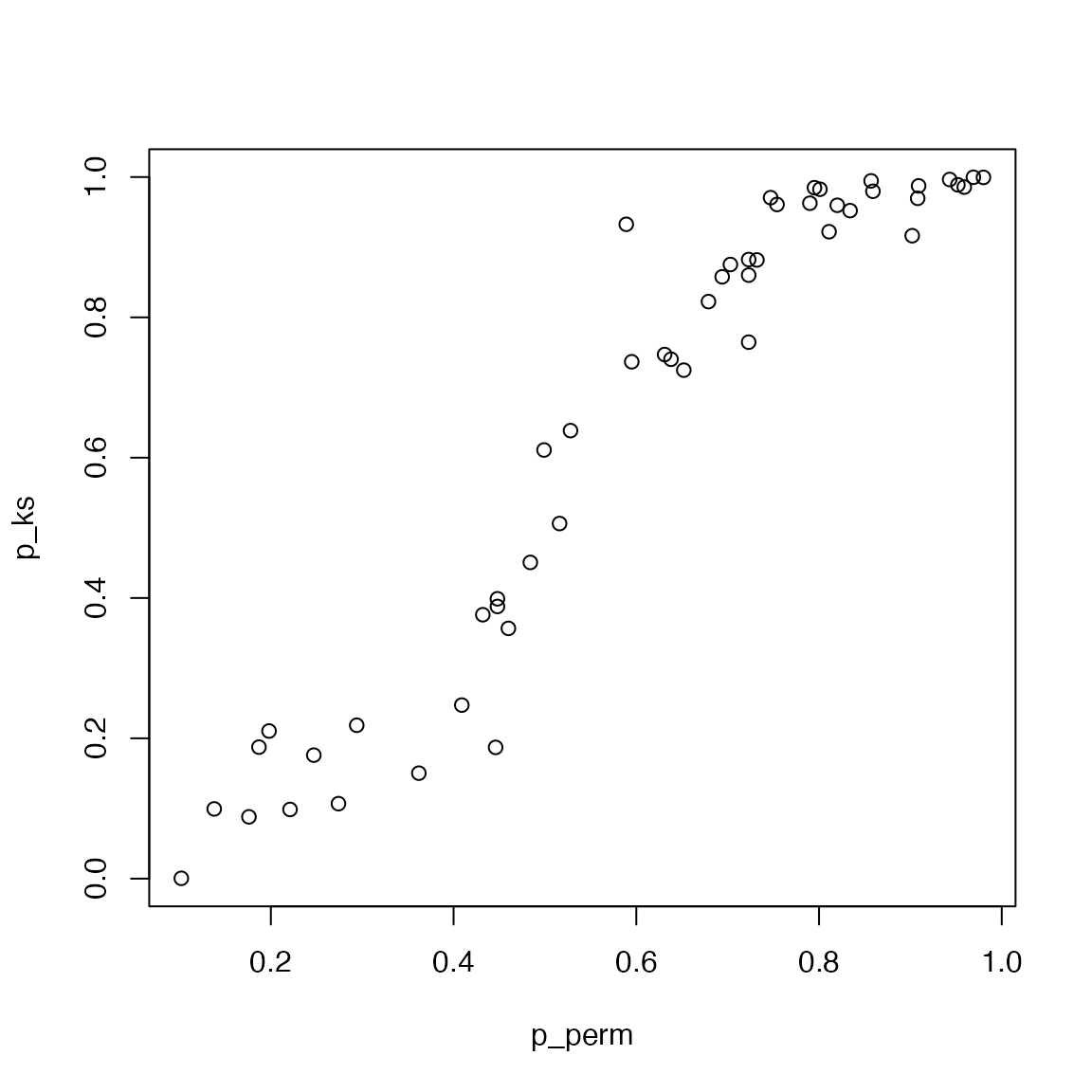
In GSEA v1, the enrichment score is basically a KS-statistics. Can you compare p-values directly from KS-test and from sample-permutation? For this comparison, use the calculate_es() for GSEA v1. Note we demonstrated the enrichment on up-regulated genes, then in ks.test(), set alternative = "great".

condition = factor(condition, levels = c("WT", "MUT"))
m1 = expr[, condition == "WT"]
m2 = expr[, condition == "MUT"]

s = (rowMeans(m1) - rowMeans(m2))/(rowSds(m1) + rowSds(m2))
s = sort(s, decreasing = TRUE)  # must be pre-sorted

p_ks = numeric(n_gs)
p_perm = numeric(n_gs)
for(i in 1:n_gs) {
    print(i)
    geneset = gs_hallmark[[i]]
    es = calculate_es(expr, condition, geneset)
    es_rand = numeric(1000)
    for(k in 1:1000) {
        es_rand[k] = calculate_es(expr, sample(condition), geneset)
    }
    p_perm[i] = sum(es_rand >= es)/1000

    l_set = names(s) %in% geneset
    l_other = !l_set
    p_ks[i] = ks.test(which(l_set), which(l_other), alternative = "greater")$p.value
}
## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5
## [1] 6
## [1] 7
## [1] 8
## [1] 9
## [1] 10
## [1] 11
## [1] 12
## [1] 13
## [1] 14
## [1] 15
## [1] 16
## [1] 17
## [1] 18
## [1] 19
## [1] 20
## [1] 21
## [1] 22
## [1] 23
## [1] 24
## [1] 25
## [1] 26
## [1] 27
## [1] 28
## [1] 29
## [1] 30
## [1] 31
## [1] 32
## [1] 33
## [1] 34
## [1] 35
## [1] 36
## [1] 37
## [1] 38
## [1] 39
## [1] 40
## [1] 41
## [1] 42
## [1] 43
## [1] 44
## [1] 45
## [1] 46
## [1] 47
## [1] 48
## [1] 49
## [1] 50
plot(p_perm, p_ks)