Skip to contents

Topic 2-05: Compare ORA and GSEA

Zuguang Gu

2025-05-31

Source: vignettes/topic2_05_compare_ORA_GSEA.Rmd
topic2_05_compare_ORA_GSEA.Rmd

There are ORA and GSEA for gene set analysis. A natural question is which one performs better? We apply ORA and GSEA on the same p53 dataset and compare the results.

library(GSEAtopics)
data(p53_dataset)
expr = p53_dataset$expr
condition = p53_dataset$condition
gs = p53_dataset$gs
s = p53_dataset$s2n

ORA

We need to perform t-test or similar DE test to extract DE genes:

We apply t-tests:

library(genefilter)
tdf = rowttests(expr, condition)
tdf$fdr = p.adjust(tdf$p.value, "BH")
sum(tdf$fdr < 0.05)
## [1] 2

It seems there are very few DE genes. We look at the distribution of the t-statistics:

plot(sort(tdf$statistic))

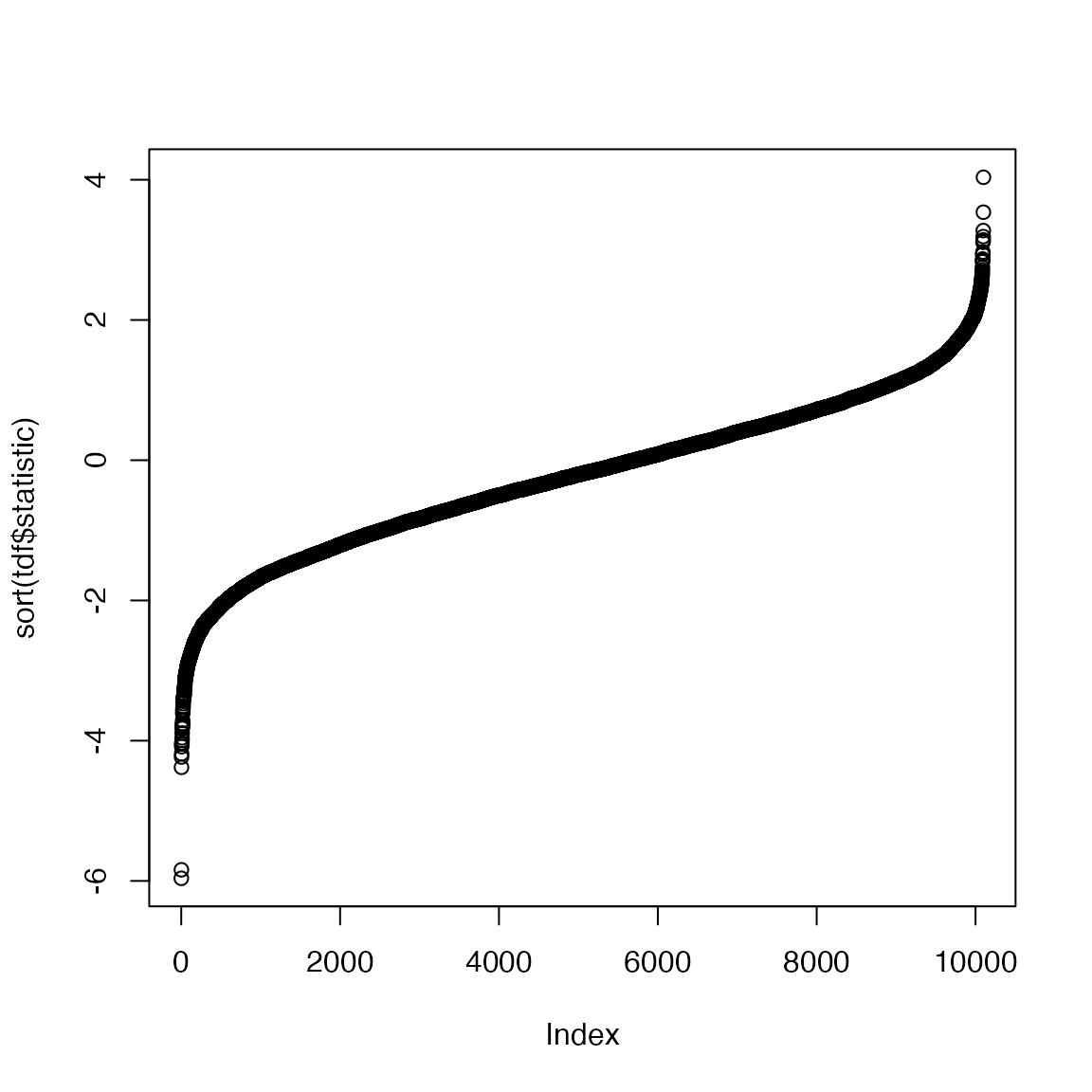
Instead of setting a cutoff for FDR, we set a cutoff for t-statistics, just to get enough number of DE genes.

sum(abs(tdf$statistic) > 2)
## [1] 728
diff = rownames(expr)[abs(tdf$statistic) > 2]

First we perform ORA using the original C2 gene sets. In the following code, we explicitly set universe to the total genes in the experiment, as we want to make the “universe genes” the same in both ORA and GSEA analysis.

tb_ora = ora(diff, gs, universe = rownames(expr))

GSEA

Next we perform GSEA using signal-to-noise ratios as gene scores.

tb_gsea = fgsea_wrapper(s, gs)

Comparison

We compare the two significant GO lists:

library(eulerr)
plot(euler(list(ORA = tb_ora$gene_set[tb_ora$p_value < 0.05], 
                GSEA = tb_gsea$gene_set[tb_gsea$p_value < 0.05])
          ), quantities = TRUE)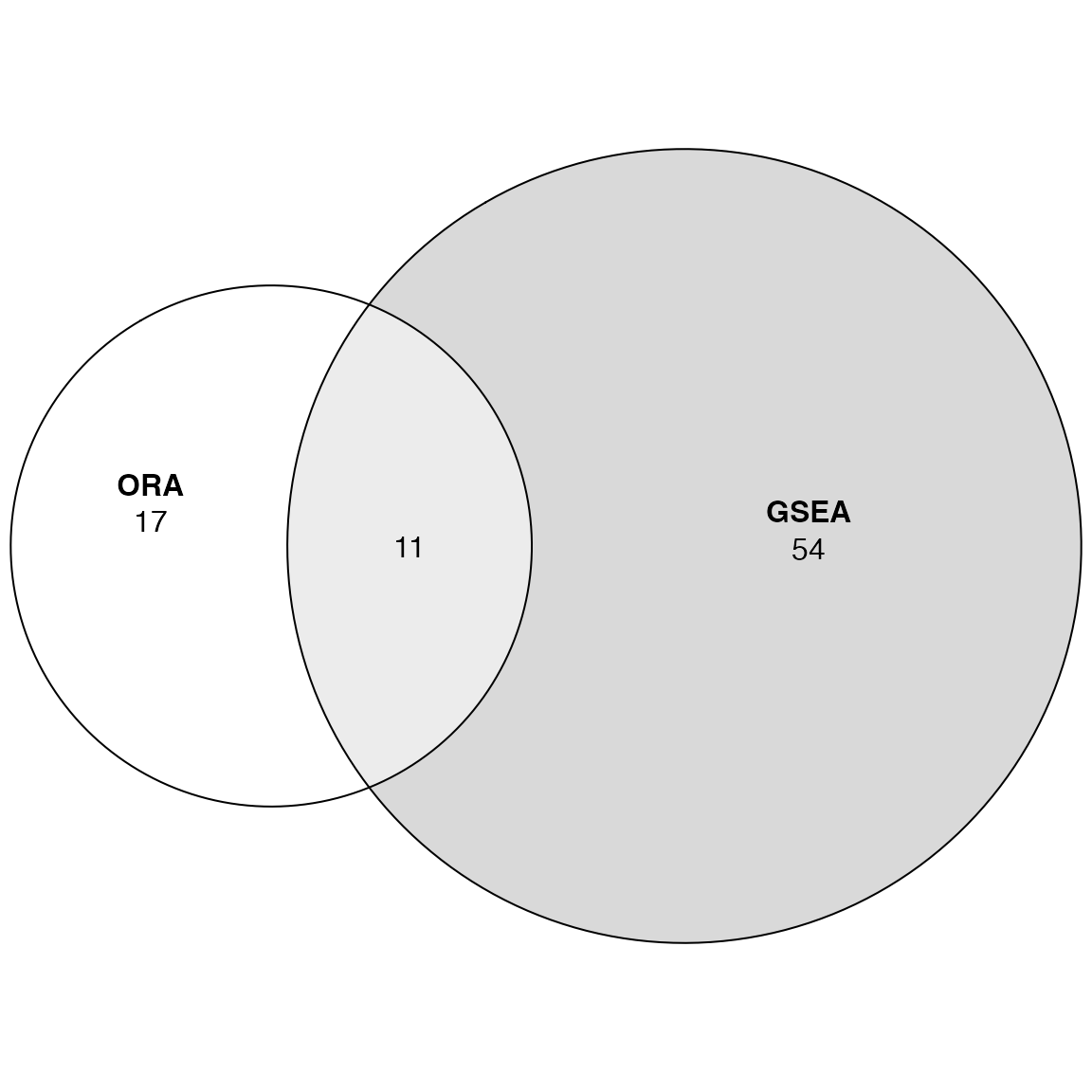

And we compare the p-values and fold enrichment from the two methods:

rownames(tb_ora) = tb_ora$gene_set
rownames(tb_gsea) = tb_gsea$gene_set
cn = intersect(rownames(tb_ora), rownames(tb_gsea))

par(mfrow = c(1, 2))
plot(tb_ora[cn, "p_value"], tb_gsea[cn, "p_value"])
plot(tb_ora[cn, "log2fe"], log2(abs(tb_gsea[cn, "nes"])))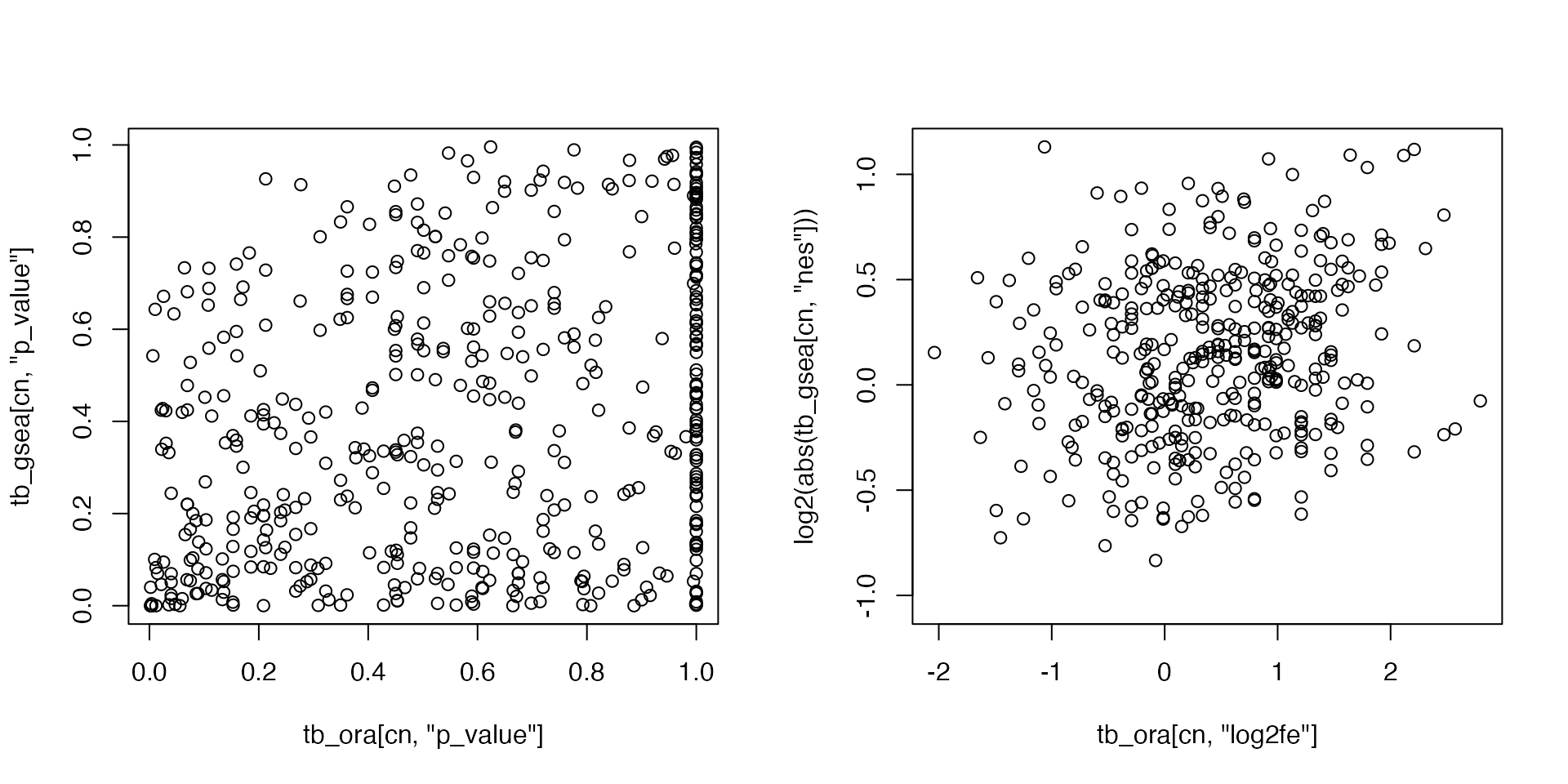

So we would say in general, ORA and GSEA are not comparible as they correspond to two different tests answering different questions.

However, they might agree very well for top-significant gene sets:

head(tb_ora)
##                              gene_set n_hits n_genes n_gs n_total   log2fe
## P53_UP                         P53_UP      9     728   40   10100 1.642270
## SA_G1_AND_S_PHASES SA_G1_AND_S_PHASES      5     728   14   10100 2.308846
## hsp27Pathway             hsp27Pathway      5     728   15   10100 2.209311
## SA_DAG1                       SA_DAG1      4     728   10   10100 2.472345
## p53Pathway                 p53Pathway      5     728   16   10100 2.116201
## gsPathway                   gsPathway      3     728    6   10100 2.794273
##                     z_score     p_value  p_adjust
## P53_UP             3.746936 0.001795847 0.4290736
## SA_G1_AND_S_PHASES 4.126911 0.002219247 0.4290736
## hsp27Pathway       3.915160 0.003133458 0.4290736
## SA_DAG1            4.011457 0.003955237 0.4290736
## p53Pathway         3.721297 0.004290736 0.4290736
## gsPathway          4.054022 0.006323397 0.5269497
head(tb_gsea)
##                                                  gene_set      p_value
## P53_UP                                             P53_UP 4.227646e-06
## hsp27Pathway                                 hsp27Pathway 7.768208e-06
## HTERT_UP                                         HTERT_UP 4.256855e-05
## GPCRs_Class_A_Rhodopsin-like GPCRs_Class_A_Rhodopsin-like 5.045670e-05
## p53hypoxiaPathway                       p53hypoxiaPathway 5.403876e-05
## p53Pathway                                     p53Pathway 5.835367e-05
##                                 p_adjust log2_p_err         es       nes n_gs
## P53_UP                       0.001910979  0.6105269 -0.5986774 -2.130912   40
## hsp27Pathway                 0.001910979  0.5933255 -0.7758925 -2.170911   15
## HTERT_UP                     0.004785001  0.5573322  0.3709129  1.859947  109
## GPCRs_Class_A_Rhodopsin-like 0.004785001  0.5573322 -0.4299558 -1.843462  111
## p53hypoxiaPathway            0.004785001  0.5573322 -0.6816006 -2.045472   20
## p53Pathway                   0.004785001  0.5573322 -0.7438596 -2.128121   16
##                              leading_edge
## P53_UP                       CDKN1A, ....
## hsp27Pathway                 TNFRSF6,....
## HTERT_UP                     AHR, DR1....
## GPCRs_Class_A_Rhodopsin-like NTSR2, A....
## p53hypoxiaPathway            CDKN1A, ....
## p53Pathway                   CDKN1A, ....

Next let’s use a larger gene set collection, the GO BP gene sets. To use the ora_go() and fgsea_go() helper functions, we need to convert genes all to EntreZ IDs.

We also do ORA using the default universe and all genes in the experiment as universe. Note the p53 dataset is very old and the total number of genes in the experiment is quite small.

tb_ora1 = ora_go(convert_to_entrez(diff))
##   gene id might be SYMBOL (p =  0.680 )
tb_ora2 = ora_go(convert_to_entrez(diff), universe = convert_to_entrez(rownames(expr)))
##   gene id might be SYMBOL (p =  0.690 )
##   gene id might be SYMBOL (p =  0.730 )
##   gene id might be SYMBOL (p =  0.640 )
lt_GO = list(ORA1 = tb_ora1$gene_set[order(tb_ora1$p_value)[1:100]], 
             ORA2 = tb_ora2$gene_set[order(tb_ora2$p_value)[1:100]], 
             GSEA = tb_gsea$gene_set[order(tb_gsea$p_value)[1:100]])
plot(euler(lt_GO), quantities = TRUE)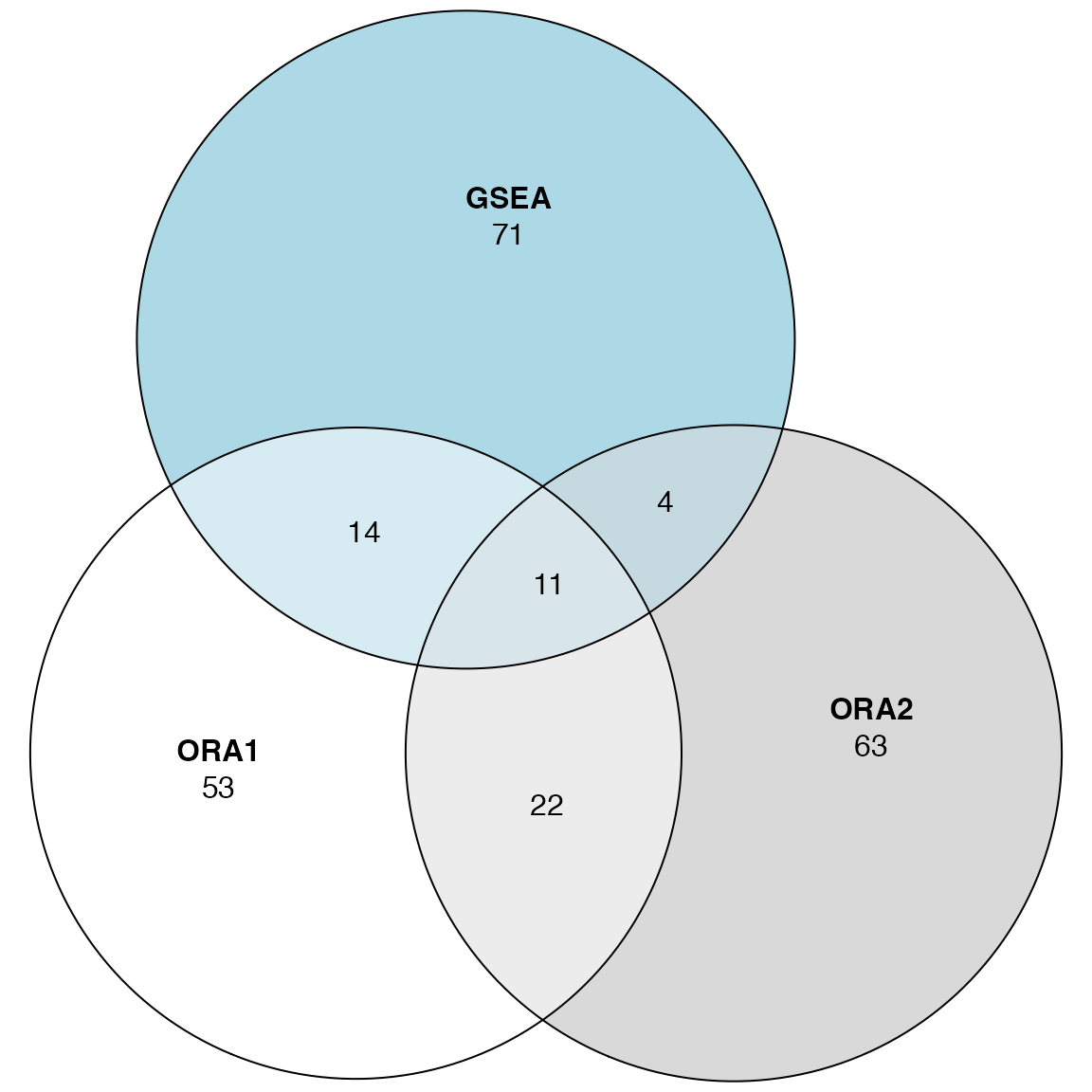

The agreement on individual is so bad, even for two ORA settings.

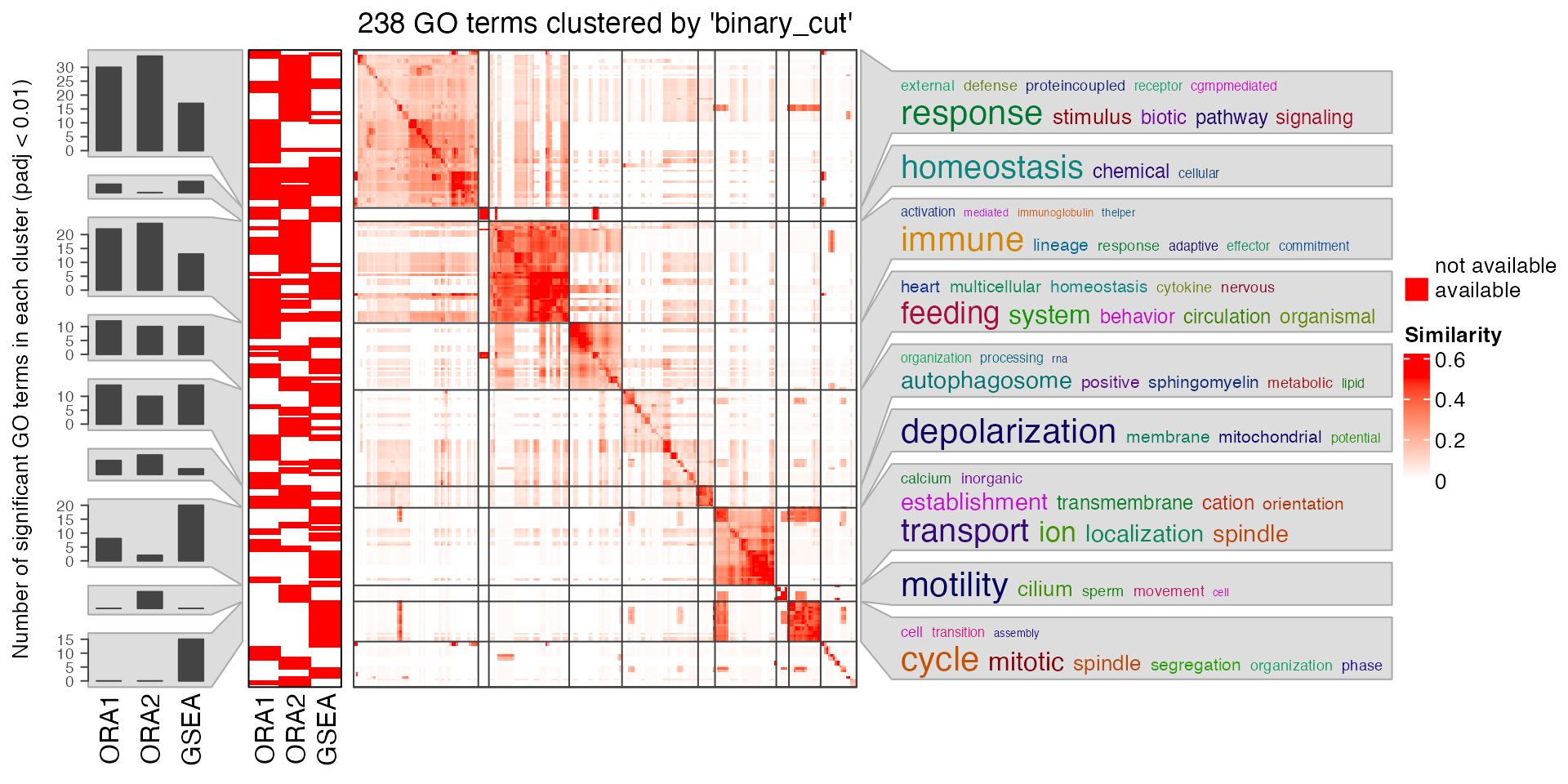
Although there are big inconsistency between different settings, but note GO has a hierarchical semantic relations, the following plot shows the general biological functions are very consistent for the three methods.